题目内容
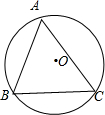 如图,⊙O是锐角△ABC的外接圆,其半径为R.BC=a,AC=b,AB=c.求证:
如图,⊙O是锐角△ABC的外接圆,其半径为R.BC=a,AC=b,AB=c.求证:| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
[提示:作直径BD,连接CD]•
考点:正弦定理与余弦定理
专题:
分析:作直径BD,连接CD,利用同弦所对的圆周角相等,可得∠A=∠D,再利用RT△BCD得出,
=sinD,可得出
=sinA,即可得出
=2R,同理可得
=2R,
=2R.即可得出
=
=
=2R.
| BC |
| BD |
| BC |
| BD |
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
解答:解:如图,作直径BD,连接CD.

∵⊙O是锐角△ABC的外接圆,
∴∠A=∠D,∠BCD=90°,
∴
=sinD,
∴
=sinA,即
=sinA,化简可得
=2R,
同理可得
=2R,
=2R.
∴
=
=
=2R.

∵⊙O是锐角△ABC的外接圆,
∴∠A=∠D,∠BCD=90°,
∴
| BC |
| BD |
∴
| BC |
| BD |
| a |
| 2R |
| a |
| sinA |
同理可得
| b |
| sinB |
| c |
| sinC |
∴
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
点评:本题考查了正弦定理和余弦定理,解答本题的关键是作辅助线构造直角三角形,利用三角函数的知识进行解答,难度适中.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 在Rt△ABC中,∠C=90°,若将各边长度都扩大为原来的2倍,则∠A的余弦值( )
在Rt△ABC中,∠C=90°,若将各边长度都扩大为原来的2倍,则∠A的余弦值( )| A、扩大2倍 | B、缩小2倍 |
| C、扩大4倍 | D、不变 |
下列图形中,不是立体图形的是( )
| A、长方体 | B、圆柱 |
| C、三角形 | D、圆锥 |
等腰三角形的两边分别为2cm,5cm,那么等腰三角形的周长为( )cm.
| A、9 | B、9或12 |
| C、12 | D、无法确定 |
若3a2-a-2=0,则5+2a-6a2=( )
| A、1 | B、-1 | C、9 | D、-9 |