题目内容
3.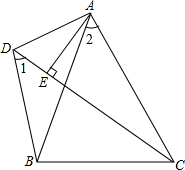 如图,在△ABC中,AB=AC,∠1=∠2,AE⊥CD于点E.
如图,在△ABC中,AB=AC,∠1=∠2,AE⊥CD于点E.求证:DC=DB=2DE.
分析 在CD上截取CM=BD,AB与CD交于点O,只要证明△ABD≌△ACM,推出AD=AM,再根据等腰三角形的性质即可解决问题.
解答  证明:如图,在CD上截取CM=BD,AB与CD交于点O.
证明:如图,在CD上截取CM=BD,AB与CD交于点O.
∵∠1=∠BAC,∠DOB=∠AOC,
∴∠ABD=∠ACM,
在△ABD和△ACM中,
$\left\{\begin{array}{l}{AB=AC}\\{∠ABC=∠ACM}\\{BD=CM}\end{array}\right.$,
∴△ABD≌△ACM,
∴AD=AM,
∵AE⊥DM,
∴DE=EM,
∴CD-BD=CM+DM-CM=2DE.
点评 本题考查等腰三角形的性质、全等三角形的判定和性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.柑橘是万州农业一大优势传统产业,柑橘产业是万州经济发展和移民安稳致富的支柱产业,也是保护三峡岸区生态环境的重要产业,做好柑橘产业发展工作意义十分重大.某水果经销商到万州采购柑橘,他看中了甲、乙两家的某种品质相近的柑橘,零售价都为6元/千克,批发价各不相同.
甲家规定:批发数量不超过100千克,全部按零售价的90%优惠;批发数量超过100千克但不超过200千克,全部按零售价的85%优惠;超过200千克的按零售价的80%优惠.
乙家的规定如下表:
(1)如果他批发80千克柑橘,则他在甲、乙两家批发各需花多少元?
(2)现在他要批发180千克柑橘,你能帮助他选择在哪家批发更优惠吗?请说明理由.
(3)如果他批发x千克柑橘(200<x<250),则他在甲、乙两家批发各需要多少元?(用含x的代数式表示)
甲家规定:批发数量不超过100千克,全部按零售价的90%优惠;批发数量超过100千克但不超过200千克,全部按零售价的85%优惠;超过200千克的按零售价的80%优惠.
乙家的规定如下表:
| 数量范围 (千克) | 0~50部分 (含50) | 50以上~150部分(含150,不含50) | 150以上~250部分(含250,不含150) | 250以上部分 (不含250) |
| 价 格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
(2)现在他要批发180千克柑橘,你能帮助他选择在哪家批发更优惠吗?请说明理由.
(3)如果他批发x千克柑橘(200<x<250),则他在甲、乙两家批发各需要多少元?(用含x的代数式表示)
13.甲、乙两人从相距24km的A、B两地沿着同一条公路相向而行,如果甲的速度是乙的速度的两倍,如果要保证在2小时以内相遇,则甲的速度( )
| A. | 小于8km/h | B. | 大于8km/h | C. | 小于4km/h | D. | 大于4km/h |
 求当a为何值时,代数式$\frac{5a+4}{6}$的值不大于代数式$\frac{7}{8}$-$\frac{1-a}{3}$的值?在数轴上表示解集,并求出满足条件的最大整数.
求当a为何值时,代数式$\frac{5a+4}{6}$的值不大于代数式$\frac{7}{8}$-$\frac{1-a}{3}$的值?在数轴上表示解集,并求出满足条件的最大整数.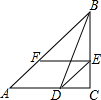 如图,在△ABC中,BD平分∠ABC交AC于点D,DE∥AB交BC于点E,EF∥AC交AB于点F,求证:BE=AF.
如图,在△ABC中,BD平分∠ABC交AC于点D,DE∥AB交BC于点E,EF∥AC交AB于点F,求证:BE=AF. 作出函数y=$\frac{2}{x+1}$的图象,并求当$\frac{1}{2}$≤x≤3时,函数的最大值和最小值.
作出函数y=$\frac{2}{x+1}$的图象,并求当$\frac{1}{2}$≤x≤3时,函数的最大值和最小值. 如图,请你在钟面上画出时针和分针,使时针和分针互相垂直,并且此时表示的时间恰好是整点.
如图,请你在钟面上画出时针和分针,使时针和分针互相垂直,并且此时表示的时间恰好是整点. 如图,已知线段a,b,求用尺规作线段a和b的比例中项.
如图,已知线段a,b,求用尺规作线段a和b的比例中项.