题目内容
9.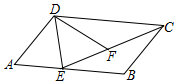 如图,在平行四边形ABCD中,E为AB边上的点,BE=BC,将△ADE沿DE翻折,点A的对应点F恰好落在CE上.∠ADF=84°,则∠BEC=32°.
如图,在平行四边形ABCD中,E为AB边上的点,BE=BC,将△ADE沿DE翻折,点A的对应点F恰好落在CE上.∠ADF=84°,则∠BEC=32°.
分析 由折叠的性质:∠DFE=∠A,设∠BEC=x,由等腰三角形的性质得出∠BCE=∠BEC=x,与平行四边形的性质得出∠A=∠BCD,AB∥CD,得出∠DCF=∠BEC=x,∠DFE=∠A=∠BCD=2x,在四边形ADFE中,由四边形内角和定理得出方程,解方程即可.
解答 解:由折叠的性质可得:∠DFE=∠A,
设∠BEC=x,
∵BE=BC,
∴∠BCE=∠BEC=x,
∵四边形ABCD是平行四边形,
∴∠A=∠BCD,AB∥CD,
∴∠DCF=∠BEC=x,
∴∠DFE=∠A=∠BCD=2x,
在四边形ADFE中,∠A+∠ADF+∠DFE+∠AEF=360°,
∴2x+84°+2x+180°-x=360°,
解得:x=32°,
∴∠BEC=32°;
故答案为:32°.
点评 此题考查了平行四边形的性质、折叠的性质、等腰三角形的性质以及四边形内角和定理.熟练掌握平行四边形的性质和折叠的性质,由四边形内角和定理得出方程是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.2016年我国就业形势总体稳定,超过全年预期目标,成为经济运行的一大亮点,城镇新增就业1312万人,这个数据用科学记数法可以表示为( )
| A. | 1.312×106人 | B. | 1.312×107人 | C. | 13.12×106人 | D. | 0.1312×108人 |
20.经统计,2016年除夕夜观看春晚直播的观众约达10.3亿人,用科学记数法表示10.3亿正确的是( )
| A. | 1.03×109 | B. | 1.03×1010 | C. | 10.3×108 | D. | 103×108 |
17.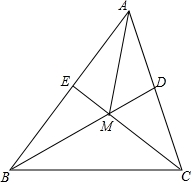 如图,已知(1)已知△ABC的两条中线BD、CE交于点M,A、D、M、E四点共圆,BC=8,则AM的长为( )
如图,已知(1)已知△ABC的两条中线BD、CE交于点M,A、D、M、E四点共圆,BC=8,则AM的长为( )
 如图,已知(1)已知△ABC的两条中线BD、CE交于点M,A、D、M、E四点共圆,BC=8,则AM的长为( )
如图,已知(1)已知△ABC的两条中线BD、CE交于点M,A、D、M、E四点共圆,BC=8,则AM的长为( )| A. | 2$\sqrt{3}$ | B. | $\frac{2}{3}$$\sqrt{3}$ | C. | $\frac{8}{3}$$\sqrt{3}$ | D. | 3$\sqrt{3}$ |
14.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (a2)3=a5 | C. | (2a+1)2=4a2+1 | D. | (-2a2b)3=-8a6b3 |
1.股票每天的涨、跌幅均不能超过10%,即当涨了原价的10%后,便不能再涨,叫做涨停;当跌了原价的10%后,便不能再跌,叫做跌停.已知一只股票某天涨停,之后两天时间又跌回到原价.若这两天此股票股价的平均下降率为x,则x满足的方程是( )
| A. | (1-x)2=$\frac{10}{11}$ | B. | (1-x)2=$\frac{9}{10}$ | C. | 1-2x=$\frac{10}{11}$ | D. | 1﹢2x=$\frac{9}{10}$ |
19.下列关于圆的切线的说法正确的是( )
| A. | 垂直于圆的半径的直线是圆的切线 | |
| B. | 与圆只有一个公共点的射线是圆的切线 | |
| C. | 经过半径的一端且垂直于半径的直线是圆的切线 | |
| D. | 如果圆心到一条直线的距离等于半径长,那么这条直线是圆的切线 |
