题目内容
18.在平面直角坐标系中,直线l:y=-$\frac{1}{2}$x+4与x轴、y轴交于B、A两点,点D,C分别为线段AB,BO的中点,如图1,将△DCB绕点B按顺时针方向旋转角α,如图2.(1)连结OC,AD,求证:△OBC∽△ABD;
(2)当0°<α<180°时,若△DCB旋转至A,C,D三点共线时,求线段OD的长;
(3)试探索:180°<α<360°时,是否还有可能存在A,C,D三点共线的情况?若存在,求出此直线的表达式;若不存在,请说明理由.

分析 (1)先确定出点A,B坐标,进而求出BD,CD,即可判断出△OBC∽△ABD;
(2)先确定出△ACB≌△BOA,进而判断出平行四边形AOBC是矩形,即可得出结论;
(3)先求出OC=$\frac{12\sqrt{5}}{5}$,进而利用勾股定理求出点C的坐标($\frac{24}{5}$,-$\frac{12}{5}$),最后用待定系数法即可得出结论.
解答 解:(1)如图1, 由y=-$\frac{1}{2}$x+4得A(0,4)点C的坐标($\frac{24}{5}$,-$\frac{12}{5}$),B(8,0),
由y=-$\frac{1}{2}$x+4得A(0,4)点C的坐标($\frac{24}{5}$,-$\frac{12}{5}$),B(8,0),
则OA=4,OB=8,
∵AD=BD,OC=BC
∴CD=$\frac{1}{2}$OA=2,BC=4,BD=$\frac{1}{2}$AB,
∴$\frac{BD}{AB}=\frac{CD}{OB}$=$\frac{1}{2}$
∵∠ABO=∠DBC,
∴∠ABO+∠ABC=∠DBC+∠ABC.
∴∠OBC=∠ABD,
∴△OBC∽△ABD.
(2)当0°<α<180°,且A,C,D三点共线时,如图2,
∵∠BCD=90°,
∴∠ACB=90°.
∴∠ACB=∠BOA=90°.
又∵OA=BC=4,AB=BA,
∴△ACB≌△BOA.
∴AC=BO.
∴四边形AOBC是平行四边形
又∵∠AOB=90°.
∴平行四边形AOBC是矩形.
∴∠AOC=90°,AC=OB=8.
∴AC=AD+CD=8+2=10.
∴OD=$\sqrt{O{A}^{2}+A{D}^{2}}$=2$\sqrt{29}$
(3)存在.
当180°<α<360°且A,C,D三点共线时,如图3,
连结OC,同(1)可得:△ABD∽△BOC.
∴$\frac{AD}{OC}=\frac{AB}{OB}=\frac{4\sqrt{5}}{8}=\frac{\sqrt{5}}{2}$
同(2)可得:△ACB≌△BOA.
∴AC=BO=8.
又CD=2,
∴AD=6.
∵$\frac{AD}{OC}=\frac{\sqrt{5}}{2}$,
∴$\frac{6}{OC}=\frac{\sqrt{5}}{2}$,
∴OC=$\frac{12\sqrt{5}}{5}$
过点C作CM⊥y轴于M,设OM=y,MC=x.
在Rt△OMC和Rt△AMC中有:
$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=(\frac{12\sqrt{5}}{5})^{2}}\\{(4+y)^{2}+{x}^{2}={8}^{2}}\end{array}\right.$解得:$\left\{\begin{array}{l}{x=\frac{24}{5}}\\{y=\frac{12}{5}}\end{array}\right.$
∴点C的坐标($\frac{24}{5}$,-$\frac{12}{5}$),
设直线AC的表达式y=kx+b
∴$\left\{\begin{array}{l}{b=4}\\{-\frac{12}{5}=\frac{24}{5}k+b}\end{array}\right.$解得:$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=4}\end{array}\right.$
所以所求直线AC的表达式为y=-$\frac{4}{3}$x+4
点评 此题是一次函数综合题,主要考查了全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,待定系数法,解(1)的关键是判断出$\frac{BD}{AB}=\frac{CD}{OB}$=$\frac{1}{2}$,解(2)的关键是判断出△ACB≌△BOA解(3)的关键是求出点C的坐标($\frac{24}{5}$,-$\frac{12}{5}$).

 如图,某校要建一个矩形花圃,花圃一边利用长为12m的墙,另外三边用25m长的篱笆围成,并在一边留一个1m宽的门,花圃面积为80m2,设与墙垂直的一边长为xm,则下列关于x的方程正确的是( )
如图,某校要建一个矩形花圃,花圃一边利用长为12m的墙,另外三边用25m长的篱笆围成,并在一边留一个1m宽的门,花圃面积为80m2,设与墙垂直的一边长为xm,则下列关于x的方程正确的是( )| A. | x(26-2x)=80 | B. | x(24-2x)=80 | C. | (x-1)(26-2x)=80 | D. | x(25-2x)=80 |
 如图,在平行四边形ABCD中,E,F分别是AB,CD边上的点,且AE=CF,求证:四边形EBFD是平行四边形.
如图,在平行四边形ABCD中,E,F分别是AB,CD边上的点,且AE=CF,求证:四边形EBFD是平行四边形.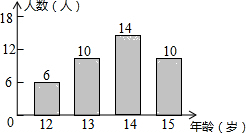 某校共有40名初中生参加足球兴趣小组,他们的年龄统计情况如图所示,则这40名学生年龄的中位数是14岁.
某校共有40名初中生参加足球兴趣小组,他们的年龄统计情况如图所示,则这40名学生年龄的中位数是14岁.