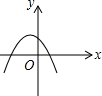题目内容
13.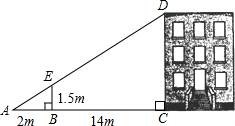 如图,利用标杆BE测量建筑物的高度,标杆BE高1.5m,测得AB=2m,BC=14m,则楼高CD为( )
如图,利用标杆BE测量建筑物的高度,标杆BE高1.5m,测得AB=2m,BC=14m,则楼高CD为( )| A. | 10.5m | B. | 9.5m | C. | 12m | D. | 14m |
分析 先根据题意得出△ABE∽△ACD,再根据相似三角形的对应边成比例即可求出CD的值.
解答 解:∵EB⊥AC,DC⊥AC,
∴EB∥DC,
∴△ABE∽△ACD,
∴$\frac{BE}{CD}$=$\frac{AB}{AC}$,
∵BE=1.5,AB=2,BC=14,
∴AC=16,
∴$\frac{1.5}{CD}$=$\frac{2}{16}$,
∴CD=12.
故选C.
点评 本题考查的是相似三角形的应用,熟知相似三角形的对应边成比例的性质是解答此题的关键.

练习册系列答案
相关题目
3.下列等式正确的是( )
| A. | 1+(-3)=$\frac{1}{3}$ | B. | -(-1)=-1 | C. | |-2|=2 | D. | (-2)×3=6 |
8.下列四个数中,最大的数是( )
| A. | (-2)2 | B. | -(-2) | C. | |-2| | D. | -|-2| |
18.在-3,0,1,-2这四个数中,是负数的有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
5.下面那个图形不能折成一个正方体( )
| A. |  | B. |  | C. |  | D. |  |
2.已知数据32,18,21,69,10,5,x的中位数为21,则下列数据中,x可以取( )
| A. | 18 | B. | 19 | C. | 20 | D. | 22 |
3.把二次函数$y=\frac{1}{2}{x^2}+4x+6$通过配方,化成y=a(x-h)2+k的形式,正确的是( )
| A. | $y=\frac{1}{2}{(x-4)^2}-2$ | B. | $y=\frac{1}{2}{(x+4)^2}+2$ | C. | $y=\frac{1}{2}{(x+4)^2}-2$ | D. | $y=\frac{1}{2}{(x-4)^2}+2$ |
 如图,正方形ABCD的边长是3cm,一个边长为1cm的小正方形沿着正方形ABCD的边AB→BC→CD→DA→AB连续地翻转,那么这个小正方形第一次回到起始位置时,小正方形中小箭头的方向是向上(填写:上、下、左、右).
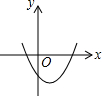
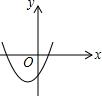
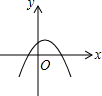
如图,正方形ABCD的边长是3cm,一个边长为1cm的小正方形沿着正方形ABCD的边AB→BC→CD→DA→AB连续地翻转,那么这个小正方形第一次回到起始位置时,小正方形中小箭头的方向是向上(填写:上、下、左、右).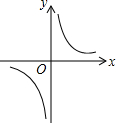 已知反比例函数y=$\frac{ab}{x}$(ab≠0)的图象如图所示,则二次函数y=ax2+bx-2的大致图象是( )
已知反比例函数y=$\frac{ab}{x}$(ab≠0)的图象如图所示,则二次函数y=ax2+bx-2的大致图象是( )