Question

【题目】如图1，点G是正方形ABCD对角线CA的延长线上任意一点，以线段AG为边作一个正方形AEFG，线段EB和GD相交于点H．

（1）求证：EB=GD且EB⊥GD；
（2）若AB=2，AG=，求的长；

（3）如图2，正方形AEFG绕点A逆时针旋转连结DE，BG，与的面积之差是否会发生变化？若不变，请求出与的面积之差；若变化，请说明理由．

Answer 1

【答案】(1)见解析； (2) ；(3)不变，与的面积之差为0

【解析】

(1)在△GAD和△EAB中，∠GAD=90°+∠EAD，∠EAB=90°+∠EAD，得到∠GAD=∠EAB，从而△EAB≌△GAD，即EB=GD；由∠AEB=∠AGD，∠EOH=∠AOG，即可得出∠EHG=∠EAG=90°；
(2)设BD与AC交于点O，由AB=AD=2，在Rt△ABD中求得DB，在Rt△GOD中利用勾股定理即可求得结果；

(3)作BQ⊥GA交GA的延长线于Q，作DP⊥EA交EA于P，可证得∠1=∠2，根据“AAS”可判断△PDA≌△QBA，所以PD=BQ，然后根据三角形面积公式得到，保持不变．

(1)如图1，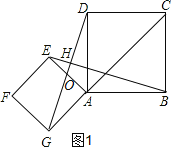

∵四边形EFGA和四边形ABCD是正方形，
∴AG=AE，AB=AD，∠EAG=90°，∠DAB=90°，

∠GAD=90°+∠EAD，∠EAB=90°+∠EAD，
∴∠GAD=∠EAB，

在△EAB和△GAD中，

，
∴△EAB≌△GAD(SAS)，
∴EB=GD；∠AEB=∠AGD，
∵∠EOH=∠AOG，
∴∠EHG=∠EAG=90°，
∴EB=GD且EB⊥GD；
(2)如图2，连接BD，BD与AC交于点O，

∵AB=AD=2，

在Rt△ABD中，，

∴AO=DO=，

∴，

∴；

(3)不变，．理由如下：

作BQ⊥GA交GA的延长线于Q，作DP⊥EA交EA于P，如图3，

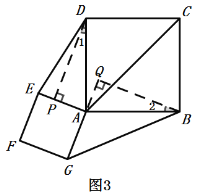
正方形ABCD和正方形AEFG中，

∠EAG=∠DAB=90°，AD=AB，

∴∠EAD+∠BAG+∠EAG+∠DAB =360，则∠BAG=180°-∠EAD，

∵∠1=90°-∠EAD，∠2=∠BAG -90°=180°-∠EAD -90°=90°-∠EAD，

∴∠1=∠2，

在△PDA和△QBA中，

，

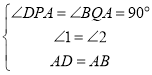∴△PDA≌△QBA(AAS)，

∴DP=BQ，

∵，，

∴．