题目内容
18.先化简:($\frac{2{x}^{2}+2x}{{x}^{2}-1}$-$\frac{{x}^{2}-x}{{x}^{2}-2x+1}$)÷$\frac{x}{x+1}$,然后解答下列问题:(1)当x=3时,求原代数式的值;
(2)原代数式的值能等于-1吗?为什么?
分析 (1)这是个分式除法与减法混合运算题,运算顺序是先做括号内的减法,此时要注意把各分子、分母先因式分解,约分后再做减法运算;做除法时要注意先把除法运算转化为乘法运算,然后约分化为最简形式,再将x=3代入计算即可;
(2)如果$\frac{x+1}{x-1}$=-1,求出x=0,此时除式$\frac{x}{x+1}$=0,原式无意义,从而得出原代数式的值不能等于-1.
解答 解:(1)($\frac{2{x}^{2}+2x}{{x}^{2}-1}$-$\frac{{x}^{2}-x}{{x}^{2}-2x+1}$)÷$\frac{x}{x+1}$
=[$\frac{2x(x+1)}{(x+1)(x-1)}$-$\frac{x(x-1)}{(x-1)^{2}}$]•$\frac{x+1}{x}$
=($\frac{2x}{x-1}$-$\frac{x}{x-1}$)•$\frac{x+1}{x}$
=$\frac{x}{x-1}$•$\frac{x+1}{x}$
=$\frac{x+1}{x-1}$.
当x=3时,原式=$\frac{3+1}{3-1}$=2;
(2)如果$\frac{x+1}{x-1}$=-1,那么x+1=-(x-1),
解得:x=0,
当x=0时,除式$\frac{x}{x+1}$=0,原式无意义,
故原代数式的值不能等于-1.
点评 本题考查了分式的化简求值.解这类题的关键是利用分解因式的方法化简分式,熟练掌握运算顺序与运算法则是解题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
8.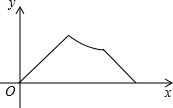 已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界逆时针匀速运动一周.设点P运动的时间为x,线段AP的长为y.表示y与x的函数关系的图象大致如图,则该封闭图形可能是( )
已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界逆时针匀速运动一周.设点P运动的时间为x,线段AP的长为y.表示y与x的函数关系的图象大致如图,则该封闭图形可能是( )
 已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界逆时针匀速运动一周.设点P运动的时间为x,线段AP的长为y.表示y与x的函数关系的图象大致如图,则该封闭图形可能是( )
已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界逆时针匀速运动一周.设点P运动的时间为x,线段AP的长为y.表示y与x的函数关系的图象大致如图,则该封闭图形可能是( )| A. |  | B. |  | C. |  | D. |  |
6.下列运算正确的是( )
| A. | (-ab2)3÷(ab2)2=-ab2 | B. | 3a+2a=5a2 | C. | (2a+b)(2a-b)=2a2-b2 | D. | (2a+b)2=4a2+b2 |
13.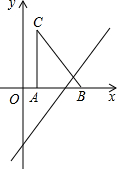 如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0).将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为( )
如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0).将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为( )
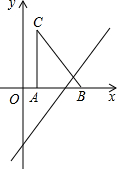 如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0).将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为( )
如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0).将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为( )| A. | 4 | B. | 8 | C. | 16 | D. | 8$\sqrt{2}$ |
8. 如图,AB=AC,BE平分∠ABC,DE∥BC,图中等腰三角形共有( )
如图,AB=AC,BE平分∠ABC,DE∥BC,图中等腰三角形共有( )
 如图,AB=AC,BE平分∠ABC,DE∥BC,图中等腰三角形共有( )
如图,AB=AC,BE平分∠ABC,DE∥BC,图中等腰三角形共有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
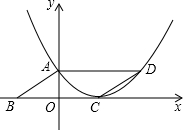 如图,在?ABCD中,BC=6,S?ABCD=12,求抛物线的解析式.
如图,在?ABCD中,BC=6,S?ABCD=12,求抛物线的解析式.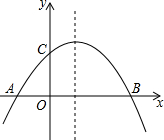 如图,已知抛物线y=-$\frac{1}{m}$(x+2)(x-m)(m>0)与x轴相交于点A、B,与y轴相交于点C,且点A在点B的左侧.
如图,已知抛物线y=-$\frac{1}{m}$(x+2)(x-m)(m>0)与x轴相交于点A、B,与y轴相交于点C,且点A在点B的左侧.