题目内容
16.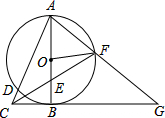 如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在$\widehat{AB}$的中点,连接AF并延长与CB的延长线相交于点G,连接OF.
如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在$\widehat{AB}$的中点,连接AF并延长与CB的延长线相交于点G,连接OF.(1)求证:OF=$\frac{1}{2}$BG;
(2)若AB=4,求DC的长.
分析 (1)直接利用圆周角定理结合平行线的判定方法得出FO是△ABG的中位线,即可得出答案;
(2)首先得出△FOE≌△CBE(ASA),则BC=FO=$\frac{1}{2}$AB=2,进而得出AC的长,再利用相似三角形的判定与性质得出DC的长.
解答 (1)证明:∵以Rt△ABC的直角边AB为直径作⊙O,点F恰好落在$\widehat{AB}$的中点,
∴$\widehat{AF}$=$\widehat{BF}$,
∴∠AOF=∠BOF,
∵∠ABC=∠ABG=90°,
∴∠AOF=∠ABG,
∴FO∥BG,
∵AO=BO,
∴FO是△ABG的中位线,
∴FO=$\frac{1}{2}$BG;
(2)解:在△FOE和△CBE中,
$\left\{\begin{array}{l}{∠FOE=∠CBE}\\{EO=BE}\\{∠OEF=∠CEB}\end{array}\right.$,
∴△FOE≌△CBE(ASA),
∴BC=FO=$\frac{1}{2}$AB=2,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=2$\sqrt{5}$,
连接DB,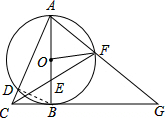 ∵AB为⊙O直径,
∵AB为⊙O直径,
∴∠ADB=90°,
∴∠ADB=∠ABC,
∵∠BCD=∠ACB,
∴△BCD∽△ACB,
∴$\frac{BC}{AC}$=$\frac{CD}{BC}$,
∴$\frac{2}{2\sqrt{5}}$=$\frac{DC}{2}$,
解得:DC=$\frac{2\sqrt{5}}{5}$.
点评 此题主要考查了相似三角形的判定与性质以及全等三角形的判定与性质等知识,正确得出△BCD∽△ACB是解题关键.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
4.由于雾霾天气频发,市场上防护口罩出现热销,某医药公司每月固定生产甲、乙两种型号的防雾霾口罩共20万只,且所有产品当月全部售出,原料成本、销售单价及工人生产提成如表:
(1)若该公司五月份的销售收入为300万元,求甲、乙两种型号的产品分别是多少万只?
(2)公司实行计件工资制,即工人每生产一只口罩获得一定金额的提成,如果公司六月份投入总成本(原料总成本+生产提成总额)不超过239万元,应怎样安排甲、乙两种型号的产量,可使该月公司所获利润最大?并求出最大利润(利润=销售收入-投入总成本)
 | 甲 | 乙 |
| 原料成本 | 12 | 8 |
| 销售单价 | 18 | 12 |
| 生产提成 | 1 | 0.8 |
(2)公司实行计件工资制,即工人每生产一只口罩获得一定金额的提成,如果公司六月份投入总成本(原料总成本+生产提成总额)不超过239万元,应怎样安排甲、乙两种型号的产量,可使该月公司所获利润最大?并求出最大利润(利润=销售收入-投入总成本)
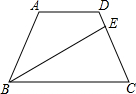 如图,在等腰梯形ABCD中,AD∥BC,AD=1,BC=3,∠ABC的平分线交腰CD于点E(不与点C、D重合).
如图,在等腰梯形ABCD中,AD∥BC,AD=1,BC=3,∠ABC的平分线交腰CD于点E(不与点C、D重合).
 如图,在△ABC中,已知∠ACB=130°,∠BAC=20°,BC=2,以点C为圆心,CB为半径的圆交AB于点D,则BD的长为2$\sqrt{3}$.
如图,在△ABC中,已知∠ACB=130°,∠BAC=20°,BC=2,以点C为圆心,CB为半径的圆交AB于点D,则BD的长为2$\sqrt{3}$.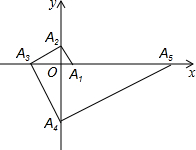 如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2016的纵坐标为-($\sqrt{3}$)2015.
如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2016的纵坐标为-($\sqrt{3}$)2015. 如图,三个正方形的边长分别为2,6,8;则图中阴影部分的面积为21.
如图,三个正方形的边长分别为2,6,8;则图中阴影部分的面积为21.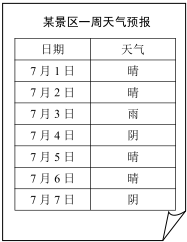 某景区7月1日-7月7日一周天气预报如图,小丽打算选择这期间的一天或两天去该景区旅游,求下列事件的概率:
某景区7月1日-7月7日一周天气预报如图,小丽打算选择这期间的一天或两天去该景区旅游,求下列事件的概率: