题目内容
7.我们定义:有一组邻角相等的凸四边形叫做“等邻角四边形”(1)概念理解:
请你根据上述定义举一个等邻角四边形的例子;
(2)问题探究:
如图1,在等邻角四边形ABCD中,∠DAB=∠ABC,AD,BC的中垂线恰好交于AB边上一点P,连结AC,BD,试探究AC与BD的数量关系,并说明理由;
(3)应用拓展:
如图2,在Rt△ABC与Rt△ABD中,∠C=∠D=90°,BC=BD=3,AB=5,将Rt△ABD绕着点A顺时针旋转角α(0°<∠α<∠BAC)得到Rt△AB′D′(如图3),当凸四边形AD′BC为等邻角四边形时,求出它的面积.

分析 (1)矩形或正方形邻角相等,满足“等邻角四边形”条件;
(2)AC=BD,理由为:连接PD,PC,如图1所示,根据PE、PF分别为AD、BC的垂直平分线,得到两对角相等,利用等角对等角得到两对角相等,进而确定出∠APC=∠DPB,利用SAS得到三角形ACB与三角形DPB全等,利用全等三角形对应边相等即可得证;
(3)分两种情况考虑:(i)当∠AD′B=∠D′BC时,延长AD′,CB交于点E,如图3(i)所示,由S四边形ACBD′=S△ACE-S△BED′,求出四边形ACBD′面积;(ii)当∠D′BC=∠ACB=90°时,过点D′作D′E⊥AC于点E,如图3(ii)所示,由S四边形ACBD′=S△AED′+S矩形ECBD′,求出四边形ACBD′面积即可.
解答 解:(1)矩形或正方形;
(2)AC=BD,理由为:
连接PD,PC,如图1所示:
∵PE是AD的垂直平分线,PF是BC的垂直平分线,
∴PA=PD,PC=PB,
∴∠PAD=∠PDA,∠PBC=∠PCB,
∴∠DPB=2∠PAD,∠APC=2∠PBC,即∠PAD=∠PBC,
∴∠APC=∠DPB,
∴△APC≌△DPB(SAS),
∴AC=BD;
(3)分两种情况考虑:
(i)当∠AD′B=∠D′BC时,延长AD′,CB交于点E,
如图3(i)所示,
∴∠ED′B=∠EBD′,
∴EB=ED′,
设EB=ED′=x,
由勾股定理得:42+(3+x)2=(4+x)2,
解得:x=4.5,
过点D′作D′F⊥CE于F,
∴D′F∥AC,
∴△ED′F∽△EAC,
∴$\frac{D′F}{AC}$=$\frac{ED′}{AE}$,即$\frac{D′F}{4}$=$\frac{4.5}{4+4.5}$,
解得:D′F=$\frac{36}{17}$,
∴S△ACE=$\frac{1}{2}$AC×EC=$\frac{1}{2}$×4×(3+4.5)=15;S△BED′=$\frac{1}{2}$BE×D′F=$\frac{1}{2}$×4.5×$\frac{36}{17}$=$\frac{81}{17}$,
则S四边形ACBD′=S△ACE-S△BED′=15-$\frac{81}{17}$=10$\frac{4}{17}$;
(ii)当∠D′BC=∠ACB=90°时,过点D′作D′E⊥AC于点E,
如图3(ii)所示,
∴四边形ECBD′是矩形,
∴ED′=BC=3,
在Rt△AED′中,根据勾股定理得:AE=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$,
∴S△AED′=$\frac{1}{2}$AE×ED′=$\frac{1}{2}$×$\sqrt{7}$×3=$\frac{3\sqrt{7}}{2}$,S矩形ECBD′=CE×CB=(4-$\sqrt{7}$)×3=12-3$\sqrt{7}$,
则S四边形ACBD′=S△AED′+S矩形ECBD′=$\frac{3\sqrt{7}}{2}$+12-3$\sqrt{7}$=12-$\frac{3\sqrt{7}}{2}$.
点评 此题属于几何变换综合题,涉及的知识有:全等三角形的判定与性质,相似三角形的判定与性质,垂直平分线定理,等腰三角形性质,以及矩形的判定与性质,熟练掌握判定与性质是解本题的关键.

 口算题天天练系列答案
口算题天天练系列答案| A. | (x2)3=x6 | B. | x2•x3=x6 | C. | x2+x3=x5 | D. | x6÷x3=x2 |
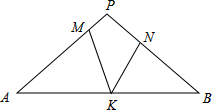 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )| A. | 44° | B. | 66° | C. | 88° | D. | 92° |
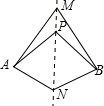 如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )
如图,直线MN是四边形AMBN的对称轴,点P是直线MN上的点,下列判断错误的是( )| A. | AM=BM | B. | AP=BN | C. | ∠MAP=∠MBP | D. | ∠ANM=∠BNM |
| A. | -a•a3=a3 | B. | -(a2)2=a4 | C. | x-$\frac{1}{3}$x=$\frac{2}{3}$ | D. | ($\sqrt{3}$-2)($\sqrt{3}$+2)=-1 |
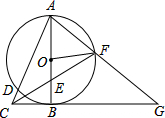 如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在$\widehat{AB}$的中点,连接AF并延长与CB的延长线相交于点G,连接OF.
如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在$\widehat{AB}$的中点,连接AF并延长与CB的延长线相交于点G,连接OF.