题目内容
11. 如图,在△ABC中,已知∠ACB=130°,∠BAC=20°,BC=2,以点C为圆心,CB为半径的圆交AB于点D,则BD的长为2$\sqrt{3}$.
如图,在△ABC中,已知∠ACB=130°,∠BAC=20°,BC=2,以点C为圆心,CB为半径的圆交AB于点D,则BD的长为2$\sqrt{3}$.
分析 如图,作CE⊥AB于E,在Rt△BCE中利用30度性质即可求出BE,再根据垂径定理可以求出BD.
解答 解:如图,作CE⊥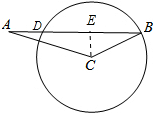 AB于E.
AB于E.
∵∠B=180°-∠A-∠ACB=180°-20°-130°=30°,
在Rt△BCE中,∵∠CEB=90°,∠B=30°,BC=2,
∴CE=$\frac{1}{2}$BC=1,BE=$\sqrt{3}$CE=$\sqrt{3}$,
∵CE⊥BD,
∴DE=EB,
∴BD=2EB=2$\sqrt{3}$.
故答案为2$\sqrt{3}$.
点评 本题考查垂径定理、三角形内角和定理等知识,解题的关键是根据垂径定理添加辅助线,记住直角三角形30度角性质,属于基础题,中考常考题型.

练习册系列答案
相关题目
2.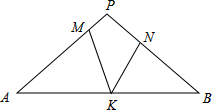 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
 如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )| A. | 44° | B. | 66° | C. | 88° | D. | 92° |
6. 如图,?ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
如图,?ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
 如图,?ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
如图,?ABCD的对角线AC、BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )| A. | 10 | B. | 14 | C. | 20 | D. | 22 |
3.门头沟位于北京西南部,属太行山余脉,地势险要“东望都邑,西走塞上而通大漠”,自古为兵家必争之地,全区总面积1455平方公里,其中山区占98.5%.将数字1455用科学记数法表示为( )
| A. | 1.455×103 | B. | 14.55×102 | C. | 1.455×104 | D. | 0.1455×104 |
1.数轴上点A、B表示的数分别是5、-3,它们之间的距离可以表示为( )
| A. | -3+5 | B. | -3-5 | C. | |-3+5| | D. | |-3-5| |
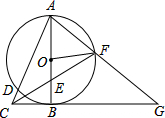 如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在$\widehat{AB}$的中点,连接AF并延长与CB的延长线相交于点G,连接OF.
如图,以Rt△ABC的直角边AB为直径作⊙O,交斜边AC于点D,点E为OB的中点,连接CE并延长交⊙O于点F,点F恰好落在$\widehat{AB}$的中点,连接AF并延长与CB的延长线相交于点G,连接OF.