题目内容
 如图,正方形ABCD的边长为2,四条弧分别以相应顶点为圆心,正方形ABCD的边长为半径.求阴影部分的面积
如图,正方形ABCD的边长为2,四条弧分别以相应顶点为圆心,正方形ABCD的边长为半径.求阴影部分的面积考点:扇形面积的计算,正方形的性质
专题:几何图形问题
分析:如解答图,作辅助线,利用图形的对称性求解.解题要点是求出弓形OmC的面积.
解答: 解:如图,设点O为弧的一个交点.
解:如图,设点O为弧的一个交点.
连接OA、OB,则△OAB为等边三角形,∴∠OBC=30°.
过点O作EF⊥CD,分别交AB、CD于点E、F,则OE为等边△OAB的高,
∴OE=
AB=
,∴OF=2-
.
过点O作PQ⊥BC,分别交AD、BC于点P、Q,则OQ=1.
S弓形OmC=S扇形OBC-S△OBC=
-
×2×1=
-1.
∴S阴影=4(S△OCD-2S弓形OmC)=4[
×2×(2-
)-2(
-1)]=16-4
-
.
故答案为:16-4
-
.
 解:如图,设点O为弧的一个交点.
解:如图,设点O为弧的一个交点.连接OA、OB,则△OAB为等边三角形,∴∠OBC=30°.
过点O作EF⊥CD,分别交AB、CD于点E、F,则OE为等边△OAB的高,
∴OE=
| ||
| 2 |
| 3 |
| 3 |
过点O作PQ⊥BC,分别交AD、BC于点P、Q,则OQ=1.
S弓形OmC=S扇形OBC-S△OBC=
| 30×π×22 |
| 360 |
| 1 |
| 2 |
| π |
| 3 |
∴S阴影=4(S△OCD-2S弓形OmC)=4[
| 1 |
| 2 |
| 3 |
| π |
| 3 |
| 3 |
| 8π |
| 3 |
故答案为:16-4
| 3 |
| 8π |
| 3 |
点评:本题考查了扇形的面积公式和正方形性质的+应用,主要考查学生的计算能力,题目比较好,难度不大.

练习册系列答案
相关题目
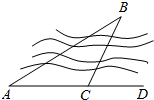 如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为( )
如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为( )| A、100米 | ||||
B、50
| ||||
C、
| ||||
| D、50米 |
 在△ABC中,分别以AB,AC为斜边作Rt△ABD和Rt△ACE,∠ADB=∠AEC=90°,∠ABD=∠ACE=30°,连接DE.若DE=5,则BC长为
在△ABC中,分别以AB,AC为斜边作Rt△ABD和Rt△ACE,∠ADB=∠AEC=90°,∠ABD=∠ACE=30°,连接DE.若DE=5,则BC长为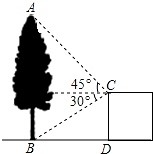 如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,则大树的高度为
如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,则大树的高度为 已知,如图,AD⊥DC,AD=4,DC=3,AB=12,问BC的长为多少时,AB⊥AC?证明你的结论.
已知,如图,AD⊥DC,AD=4,DC=3,AB=12,问BC的长为多少时,AB⊥AC?证明你的结论.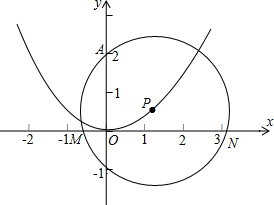 如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和(
如图,抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和(