题目内容
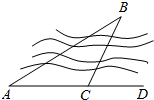 如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为( )
如图,要测量B点到河岸AD的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=100米,则B点到河岸AD的距离为( )| A、100米 | ||||
B、50
| ||||
C、
| ||||
| D、50米 |
考点:解直角三角形的应用
专题:几何图形问题
分析:过B作BM⊥AD,根据三角形内角与外角的关系可得∠ABC=30°,再根据等角对等边可得BC=AC,然后再计算出∠CBM的度数,进而得到CM长,最后利用勾股定理可得答案.
解答: 解:过B作BM⊥AD,
解:过B作BM⊥AD,
∵∠BAD=30°,∠BCD=60°,
∴∠ABC=30°,
∴AC=CB=100米,
∵BM⊥AD,
∴∠BMC=90°,
∴∠CBM=30°,
∴CM=
BC=50米,
∴BM=
CM=50
米,
故选:B.
 解:过B作BM⊥AD,
解:过B作BM⊥AD,∵∠BAD=30°,∠BCD=60°,
∴∠ABC=30°,
∴AC=CB=100米,
∵BM⊥AD,
∴∠BMC=90°,
∴∠CBM=30°,
∴CM=
| 1 |
| 2 |
∴BM=
| 3 |
| 3 |
故选:B.
点评:此题主要考查了解直角三角形的应用,关键是证明AC=BC,掌握直角三角形的性质:30°角所对直角边等于斜边的一半.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9的相反数是( )
| A、-9 | ||
| B、9 | ||
| C、±9 | ||
D、
|
一组数据,6、4、a、3、2的平均数是5,这组数据的方差为( )
| A、8 | ||
| B、5 | ||
C、2
| ||
| D、3 |
 如图,正方形ABCD的边长为2,四条弧分别以相应顶点为圆心,正方形ABCD的边长为半径.求阴影部分的面积
如图,正方形ABCD的边长为2,四条弧分别以相应顶点为圆心,正方形ABCD的边长为半径.求阴影部分的面积 如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF.
如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF.