题目内容
7.计算:$\sqrt{27}-9\sqrt{\frac{1}{3}}+$($\frac{1}{3}$)-2=9.分析 先进行二次根式的化简,然后合并.
解答 解:原式=3$\sqrt{3}$-3$\sqrt{3}$+9
=9.
故答案为:9.
点评 本题考查了二次根式的加减法,解答本题的关键是掌握二次根式的化简以及合并.

练习册系列答案
相关题目
12.用配方法解方程${x^2}-\frac{2}{3}x-1=0$应该先变形为( )
| A. | ${(x-\frac{1}{3})^2}=\frac{8}{9}$ | B. | ${(x-\frac{1}{3})^2}=-\frac{8}{9}$ | C. | ${(x-\frac{1}{3})^2}=\frac{10}{9}$ | D. | ${(x-\frac{2}{3})^2}=0$ |
17.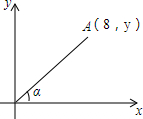 如图,在平面直角坐标系中,点A在第一象限,其坐标为(8,y),且OA与x轴正半轴的夹角α的正切值为$\frac{3}{4}$,则y的值为( )
如图,在平面直角坐标系中,点A在第一象限,其坐标为(8,y),且OA与x轴正半轴的夹角α的正切值为$\frac{3}{4}$,则y的值为( )
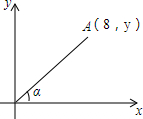 如图,在平面直角坐标系中,点A在第一象限,其坐标为(8,y),且OA与x轴正半轴的夹角α的正切值为$\frac{3}{4}$,则y的值为( )
如图,在平面直角坐标系中,点A在第一象限,其坐标为(8,y),且OA与x轴正半轴的夹角α的正切值为$\frac{3}{4}$,则y的值为( )| A. | 4 | B. | $\frac{9}{2}$ | C. | 5 | D. | 6 |
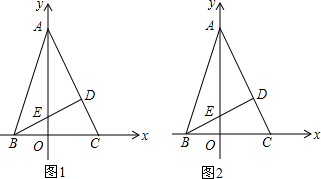
 如图,在正方形ABCD中,AB=12,E是AB边上一点,且AE=3BE,P是对角线AC上一动点,则PB+PE的最小值是15.
如图,在正方形ABCD中,AB=12,E是AB边上一点,且AE=3BE,P是对角线AC上一动点,则PB+PE的最小值是15.