题目内容
17.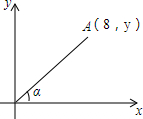 如图,在平面直角坐标系中,点A在第一象限,其坐标为(8,y),且OA与x轴正半轴的夹角α的正切值为$\frac{3}{4}$,则y的值为( )
如图,在平面直角坐标系中,点A在第一象限,其坐标为(8,y),且OA与x轴正半轴的夹角α的正切值为$\frac{3}{4}$,则y的值为( )| A. | 4 | B. | $\frac{9}{2}$ | C. | 5 | D. | 6 |
分析 由点A作辅助线AB⊥x轴于点B,由点A在第一象限,其坐标为(8,y),且OA与x轴正半轴的夹角α的正切值为$\frac{3}{4}$,可得y的值.
解答 解:作AB⊥x轴于点B,如下图所示:
∵tanα=$\frac{3}{4}$,tanα=$\frac{y}{8}$,
∴y=6.
故选项A错误,选项B错误,选项C错误,选项D正确.
故选D.
点评 本题考查解直角三角函数、坐标与图形的性质,解题的关键是能用数形结合的思想将题目中的已知条件和图形联系在一起.

练习册系列答案
相关题目
8.下列各组的三条线段中,不能组成三角形的是( )
| A. | 2,2,1 | B. | 5,2,4 | C. | 1,1,2 | D. | 5,6,7 |
9.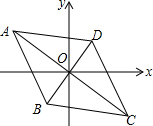 如图,菱形ABCD的对角线相交于坐标原点,点A的坐标为(a,2),点B的坐标为(-1,-$\sqrt{3}$),点C的坐标为(2$\sqrt{3}$,c),那么a,c的值分别是( )
如图,菱形ABCD的对角线相交于坐标原点,点A的坐标为(a,2),点B的坐标为(-1,-$\sqrt{3}$),点C的坐标为(2$\sqrt{3}$,c),那么a,c的值分别是( )
 如图,菱形ABCD的对角线相交于坐标原点,点A的坐标为(a,2),点B的坐标为(-1,-$\sqrt{3}$),点C的坐标为(2$\sqrt{3}$,c),那么a,c的值分别是( )
如图,菱形ABCD的对角线相交于坐标原点,点A的坐标为(a,2),点B的坐标为(-1,-$\sqrt{3}$),点C的坐标为(2$\sqrt{3}$,c),那么a,c的值分别是( )| A. | a=-1,c=-$\sqrt{3}$ | B. | a=-2$\sqrt{3}$,c=-2 | C. | a=1,c=$\sqrt{3}$ | D. | a=2$\sqrt{3}$,c=2 |
7.已知点(-2,y1),(3,y2)都在直线y=kx-1上,且k小于0,则y1与y2的大小关系是( )
| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 不能比较 |
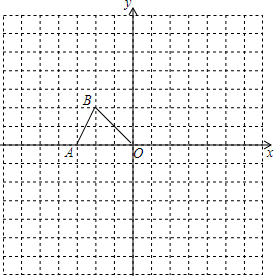 如图,在平面直角坐标系中,△AOB的位置如图所示,图中小正方形的边长均为1,请画出△AOB以点O为位似中心,放大到原来的2倍的位似图形,并写出放大后三角形三个顶点的坐标.
如图,在平面直角坐标系中,△AOB的位置如图所示,图中小正方形的边长均为1,请画出△AOB以点O为位似中心,放大到原来的2倍的位似图形,并写出放大后三角形三个顶点的坐标. 如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,以下结论:①∠BAC=70°;②∠DOC=90°;③∠BDC=35°;④∠DAC=55°,其中正确的是①③④.(填写序号)
如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,以下结论:①∠BAC=70°;②∠DOC=90°;③∠BDC=35°;④∠DAC=55°,其中正确的是①③④.(填写序号)