题目内容
8.若方程组$\left\{\begin{array}{l}{2x+y=b}\\{x-y=a}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$,则直线y=-2x+b与直线y=x-a的交点坐标是(-1,3).分析 根据两个函数图象的交点就是两个函数组成的方程组的解可得答案.
解答 解:因为方程组$\left\{\begin{array}{l}{2x+y=b}\\{x-y=a}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$,
所以直线y=-2x+b与直线y=x-a的交点坐标是(-1,3),
故答案为:(-1,3),
点评 此题主要考查了二元一次方程(组)与一次函数的关系,关键是掌握两条直线的交点坐标应该是联立两个一次函数解析式所组方程组的解.

练习册系列答案
相关题目
4.下列各组数中,作为三角形三边长,能构成直角三角形的一组是( )
| A. | $\sqrt{3}$,2,$\sqrt{5}$ | B. | 3,4,6 | C. | 1,$\sqrt{3}$,2 | D. | 6,8,12 |
16.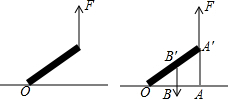 如图,慢慢将电线杆竖起,如果所用力F的方向始终竖直向上,则电线杆竖起过程中所用力的大小将( )
如图,慢慢将电线杆竖起,如果所用力F的方向始终竖直向上,则电线杆竖起过程中所用力的大小将( )
 如图,慢慢将电线杆竖起,如果所用力F的方向始终竖直向上,则电线杆竖起过程中所用力的大小将( )
如图,慢慢将电线杆竖起,如果所用力F的方向始终竖直向上,则电线杆竖起过程中所用力的大小将( )| A. | 变大 | B. | 变小 | C. | 不变 | D. | 无法判断 |
20.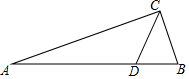 如图所示,在Rt△ABC中,斜边AB=3,BC=1,点D在AB上,且$\frac{BD}{AD}$=$\frac{1}{3}$,则tan∠BCD的值是( )
如图所示,在Rt△ABC中,斜边AB=3,BC=1,点D在AB上,且$\frac{BD}{AD}$=$\frac{1}{3}$,则tan∠BCD的值是( )
 如图所示,在Rt△ABC中,斜边AB=3,BC=1,点D在AB上,且$\frac{BD}{AD}$=$\frac{1}{3}$,则tan∠BCD的值是( )
如图所示,在Rt△ABC中,斜边AB=3,BC=1,点D在AB上,且$\frac{BD}{AD}$=$\frac{1}{3}$,则tan∠BCD的值是( )| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{3\sqrt{3}}{2}$ |
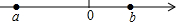 如图:a,b是数轴上的两点,化简$\sqrt{{a^2}-2ab+{b^2}}$+$\sqrt{{a^2}+2ab+{b^2}}$=-2a.
如图:a,b是数轴上的两点,化简$\sqrt{{a^2}-2ab+{b^2}}$+$\sqrt{{a^2}+2ab+{b^2}}$=-2a. 知不等式组$\left\{\begin{array}{l}x+2a≥1\\ 2x-b<3\end{array}$的解集如图所示,则a-b的值为0.
知不等式组$\left\{\begin{array}{l}x+2a≥1\\ 2x-b<3\end{array}$的解集如图所示,则a-b的值为0. 如图,D、E分别是△ABC的边AB、AC的中点,连接CD、DE,若△ADE的面积为2,则△ABC的面积为8.
如图,D、E分别是△ABC的边AB、AC的中点,连接CD、DE,若△ADE的面积为2,则△ABC的面积为8. 二次函数y=ax2+bx+c的图象如图所示,已知点A(2,y1),B(-5,y2)和C(-7,y3)都在此图象上,则y1,y2,y3的大小关系是y2>y3>y1.
二次函数y=ax2+bx+c的图象如图所示,已知点A(2,y1),B(-5,y2)和C(-7,y3)都在此图象上,则y1,y2,y3的大小关系是y2>y3>y1. 如图,直线AB与CD相交于点O,射线OE平分∠BOD,若∠DOE=20°,则∠AOC=40°,∠BOC=140°.
如图,直线AB与CD相交于点O,射线OE平分∠BOD,若∠DOE=20°,则∠AOC=40°,∠BOC=140°.