题目内容
5．
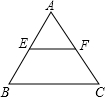如图所示，刘伯伯家有一块等边三角形的空地ABC，已知E，F分别是边AB，AC的中点，量得EF=5米，他想把四边形BCFE用篱笆围起来放养小鸡，则需用篱笆的长是25 米．
分析 根据三角形中位线定理计算即可．
解答 解：∵E，F分别是边AB，AC的中点，
∴BC=2EF=10（米），
∵△ABC是等边三角形，
∴BE=CF=5（米），
∴四边形BCFE的周长为：BC+BE+CF+EF=25（米），
故答案为：25．
点评 本题考查的是三角形中位线定理，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键．
练习册系列答案
相关题目
16．
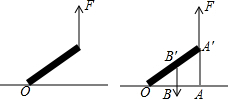如图，慢慢将电线杆竖起，如果所用力F的方向始终竖直向上，则电线杆竖起过程中所用力的大小将（ ）
如图，慢慢将电线杆竖起，如果所用力F的方向始终竖直向上，则电线杆竖起过程中所用力的大小将（ ）| A． | 变大 | B． | 变小 | C． | 不变 | D． | 无法判断 |
如图，D、E分别是△ABC的边AB、AC的中点，连接CD、DE，若△ADE的面积为2，则△ABC的面积为8．
20．
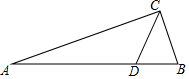如图所示，在Rt△ABC中，斜边AB=3，BC=1，点D在AB上，且$\frac{BD}{AD}$=$\frac{1}{3}$，则tan∠BCD的值是（ ）
如图所示，在Rt△ABC中，斜边AB=3，BC=1，点D在AB上，且$\frac{BD}{AD}$=$\frac{1}{3}$，则tan∠BCD的值是（ ）| A． | $\frac{1}{3}$ | B． | 1 | C． | $\frac{2\sqrt{2}}{3}$ | D． | $\frac{3\sqrt{3}}{2}$ |
10．
如图，在半径为2的⊙O中，∠AOB=45°，AC是直径，点B在圆上，$\sqrt{2}$≈1.4，则tanC近似值为（精确到0.1）（ ）
如图，在半径为2的⊙O中，∠AOB=45°，AC是直径，点B在圆上，$\sqrt{2}$≈1.4，则tanC近似值为（精确到0.1）（ ）| A． | 0.4 | B． | 0.7 | C． | 1.4 | D． | 2.4 |
二次函数y=ax2+bx+c的图象如图所示，已知点A（2，y1），B（-5，y2）和C（-7，y3）都在此图象上，则y1，y2，y3的大小关系是y2＞y3＞y1．
15．下列以a，b，c为三边的三角形中，是直角三角形的是（ ）
| A． | $a=\sqrt{3}$，$b=\sqrt{4}$，$c=\sqrt{5}$ | B． | a=1，b=2，$c=2\sqrt{5}$ | C． | a=2，b=3，$c=\sqrt{5}$ | D． | a=1，$b=2\sqrt{2}$，c=2 |