题目内容
16.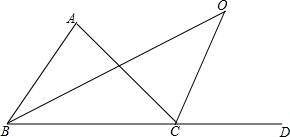 如图,∠ACD是△ABC的外角,∠ABC与∠ACD的角平分线交于点O.
如图,∠ACD是△ABC的外角,∠ABC与∠ACD的角平分线交于点O.(1)若∠ABC=66°,∠ACB=34°,则∠A=80°,∠O=40°;
(2)探索∠A与∠O的数量关系,并说明理由;
(3)若AB∥CO,AC⊥BO,求∠ACB的度数.
分析 (1)由三角形内角和定理可求∠A,求出∠OBC,和∠BCO,再由三角形内角和定理即可求出结论;
(2)由题中角平分线可得∠O=∠OCD-∠OBC=$\frac{1}{2}$∠ACD-$\frac{1}{2}$∠ABC,进而得出∠A=180°-∠ABC-180°+∠ACD=∠ACD-∠ABC,即可得出结论;
(3)AC与BO交于点E,由OC∥AB,证得∠ABO=∠O,由AC⊥BO,证得∠AEB=90°,故2∠O+∠O=90°,进而证得∠A=60°,∠ABC=2∠ABO即可证得结论.
解答 解:(1)∵∠ABC=66°,∠ACB=34°,
∴∠A=180°-∠ABC-∠ACB=80°,
∵∠ABC与∠ACD的角平分线交于点O,
∴∠OBC=$\frac{1}{2}$∠ABC=33°,∠OCD=$\frac{1}{2}$(180°-34°)=73°,
∴∠O=∠OCD-∠OBC=40°,
故答案为:80、40;
(2)∵BO平分∠ABC,
∴∠ABO=$\frac{1}{2}$∠ABC,
∵CO平分∠ACD,
∴∠ACO=$\frac{1}{2}$∠ACD,
∵∠AEB=∠CEO,
∵∠A+∠ABO=∠O+∠ACO,
∴∠A+∠ABO=∠O+$\frac{1}{2}$∠ACD,
∵∠ACD是△ABC的外角,
∴∠ACD=∠A+∠ABC=∠A+2∠ABO,
∴∠A+∠ABO=∠O+$\frac{1}{2}$∠A+∠ABO,
∴$\frac{1}{2}$∠A=∠O;
(3)如图,AC与BO交于点E,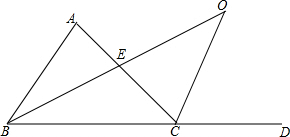
∵OC∥AB,
∴∠ABO=∠O,
∵AC⊥BO,
∴∠AEB=90°,
∴∠A+∠ABO=90°,
∴2∠O+∠O=90°,
∴∠O=30°,
∴∠A=60°,∠ABC=2∠ABO=60°,
∴∠ACB=60°.
点评 本题主要考查了三角形的内角和定理以及外角的性质问题,平行线的性质,能够掌握并熟练运用平行线的性质是解决问题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 等边三角形 | B. | 直角三角形 | C. | 平行四边形 | D. | 菱形 |
| A. | -3 | B. | 2 | C. | -1 | D. | 0 |
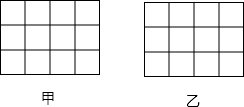 如图,正方形网格中的每个小正方形=边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图.
如图,正方形网格中的每个小正方形=边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画图.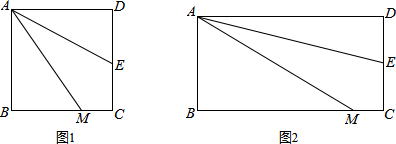
 如图,是将一个长方体沿它的对角线切去一半后剩下的部分.
如图,是将一个长方体沿它的对角线切去一半后剩下的部分.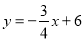 与
与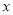 轴、
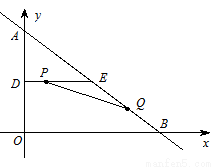
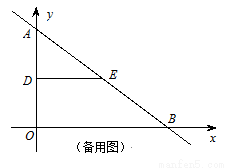
轴、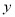 轴分别交于点B、 A,点D、E分别是AO、AB的中点,连接DE,点P从点D出发,沿DE方向匀速运动,速度为1cm/s;与此同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为
轴分别交于点B、 A,点D、E分别是AO、AB的中点,连接DE,点P从点D出发,沿DE方向匀速运动,速度为1cm/s;与此同时,点Q从点B出发,沿BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为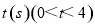 .
.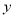 (cm2),求y与t之间的函数关系式;
(cm2),求y与t之间的函数关系式;