题目内容
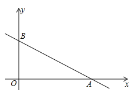
【题目】定义:对于给定的一次函数y=ax+b(a≠0),把形如![]() 的函数称为一次函数y=ax+b(a≠0)的衍生函数.已知矩形ABCD的顶点坐标分别为A(1,0),B(1,2),C(-3,2),D(-3,0).
的函数称为一次函数y=ax+b(a≠0)的衍生函数.已知矩形ABCD的顶点坐标分别为A(1,0),B(1,2),C(-3,2),D(-3,0).
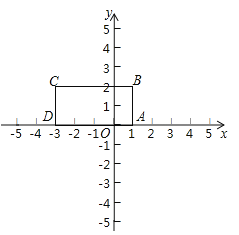
(1)已知函数y=2x+l.
①若点P(-1,m)在这个一次函数的衍生函数图像上,则m= .
②这个一次函数的衍生函数图像与矩形ABCD的边的交点坐标分别为 .
(2)当函数y=kx-3(k>0)的衍生函数的图象与矩形ABCD有2个交点时,k的取值范围是 .
【答案】(1)①3,②(![]() ,2)或(
,2)或(![]() ,,0);(2)1<k<3;
,,0);(2)1<k<3;
【解析】
(1)①x=-1<0,则m=-2×(-1)+1=3,即可求解;②一次函数的衍生函数图象与矩形ABCD的边的交点位置在BC和AD上,即可求解;
(2)当直线在位置①时,函数和矩形有1个交点,当直线在位置②时,函数和图象有3个交点,在图①②之间的位置,直线与矩形有2个交点,即可求解.
解:(1)①x=-1<0,则m=-2×(-1)+1=3,
故答案为:3;
②一次函数的衍生函数图象与矩形ABCD的边的交点位置在BC和AD上,
当y=2时,2x+1=2,解得:x=![]() ,
,
当y=0时,2x+1=0,解得:x=![]() ,
,
故答案为:(![]() ,2)或(
,2)或(![]() ,,0);
,,0);
(2)函数可以表示为:y=|k|x-3,
如图所示当直线在位置①时,函数和矩形有1个交点,

当x=3时,y=|k|x-3=3|k|-3=0,k=±1,
k>0,取k=1
当直线在位置②时,函数和图象有3个交点,
同理k=3,
故在图①②之间的位置,直线与矩形有2个交点,
即:1<k<3.

练习册系列答案
相关题目