题目内容
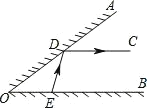
【题目】如图， AOB 的一边 OA 为平面镜， AOB 37°36 ，在 OB 上有一点 E ，从 E 点射出 一束光线经 OA 上一点 D 反射，反射光线 DC 恰好与 OB 平行，则 DEB 的度数是_°．
【答案】75.2
【解析】
过点D作DF垂直AO交OB于点F,根据题意知,DF是∠CDE的角平分线，故∠1=∠3;然后又由两直线CD∥OB推知内错角∠1=∠2;最后由三角形的内角和定理求得∠DEB的度数.
解:过点D作DF⊥AO交OB于点F.
∵入射角等于反射角
∴∠1=∠3
∵CD∥OB
∴∠1=∠2(两直线平行,内错角相等)
∴∠2=∠3(等量代换)
在Rt△DOF中,∠ODF=90°,∠AOB=37°36′
∴∠2=90°-37°36′=52°24′
∴在△DEF中，∠DEB=180°-2∠2=75°12′=75.2°
故答案为75.2.
练习册系列答案
相关题目
