题目内容
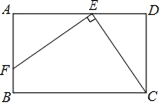
【题目】如图，点E、F分别在矩形ABCD的两条边上，且EF⊥EC，EF=EC，若该矩形的周长为16，AE=3，则DE的长为（ ）
A. 
B. 2 C. 
D. 3
【答案】B
【解析】分析：先证∠AEF=∠ECD，再证△AEF≌△DCE，然后结合题目中已知的线段关系可求出AD+DC=8，进而可求出DE的长．
详解：在Rt△AEF和Rt△DEC中，EF⊥CE．
∴∠FEC=90°．
∴∠AEF+∠DEC=90°．
而∠ECD+∠DEC=90°．
∴∠AEF=∠ECD，
在△AEF与△DCE中，
,
∴△AEF≌△DCE（AAS）．
∴AE=CD=3，
∵矩形ABCD的周长为16cm．
∴2（AE+ED+DC）=32，即2（6+DE）=16，
解得：DE=2．
故选B．
练习册系列答案
相关题目
【题目】某批彩色弹力球的质量检验结果如下表：
抽取的彩色弹力球数n | 500 | 1000 | 1500 | 2000 | 2500 |
优等品频数m | 471 | 946 | 1426 | 1898 | 2370 |
优等品频率 | 0.942 | 0.946 | 0.951 | 0.949 | 0.948 |
（1）请在图中完成这批彩色弹力球“优等品”频率的折线统计图
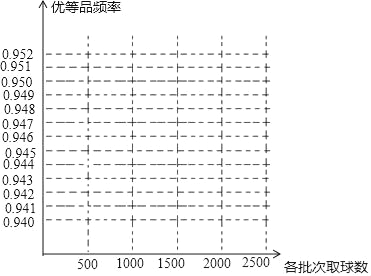
（2）这批彩色弹力球“优等品”概率的估计值大约是多少？（精确到0.01）
（3）从这批彩色弹力球中选择5个黄球、13个黑球、22个红球，它们除了颜色外都相同，将它们放入一个不透明的袋子中，求从袋子中摸出一个球是黄球的概率．
（4）现从第（3）问所说的袋子中取出若干个黑球，并放入相同数量的黄球，搅拌均匀，使从袋子中摸出一个黄球的概率为
，求取出了多少个黑球？
