Question

P为⊙O外一点，PA、PB分别切⊙O于A、B点，若∠APB=2α，⊙O的半径为R，则AB的长为（　　）

• A．

  Rsinα

  tanα

• B．

  Rtanα

  sinα

• C．

  2Rsinα

  tanα

• D．

  2Rtanα

  sinα

Answer 1

分析：由PA与PB为圆O的两条切线，利用切线长定理得到PA=PB，PA与OA垂直，PB与OB垂直，利用HL证明Rt△AOP≌△BOP，利用全等三角形的对应角相等得到∠APO=∠BPO，再由∠APB=2α，得到∠APO=∠BPO=α，在Rt△AOP中，利用正切函数定义及OA=R表示出AP，利用三线合一得到Q为AB的中点，OP与AB垂直，在Rt△APQ中，利用正弦函数公式表示出AQ，由AB=2AQ即可表示出AB，得到正确的选项．

解答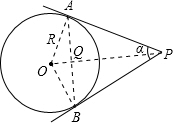：解：∵PA、PB分别切⊙O于A、B点，
∴PA=PB，∠PAO=∠PBO=90°，
在Rt△AOP和△BOP中，

PA=PB OP=OP

，
∴Rt△AOP≌△BOP（HL），又∠APB=2α，
∴∠APO=∠BPO=α，∠AOP=∠BOP，
∵OA=OB，
∴OP⊥AB，AQ=BQ，
在Rt△AOP中，OA=R，∠APO=α，
∴tanα=

OA

AP

，即AP=

R

tanα

，
在Rt△AQP中，∠APO=α，AP=

R

tanα

，
∴sinα=

AQ

AP

，即AQ=

Rsinα

tanα

，
则AB=2AQ=

2Rsinα

tanα

．
故选C．

点评：此题考查了切线的性质，切线长定理，锐角三角函数定义，全等三角形的判定与性质，以及等腰三角形的性质，熟练掌握切线的性质是解本题的关键．