题目内容
P为⊙O外一点,PA,PB分别切⊙O于点A,B,∠APB=50°,点C为⊙O上一点(不与A,B重合),则∠ACB的度数为分析:连接OA、OB,根据切线的性质判断出∠OAP的度数,∠OBP的度数;再根据四边形的内角和是360°,求出
∠ACB的度数,最后由圆内接四边形的性质,求出∠D的度数.
∠ACB的度数,最后由圆内接四边形的性质,求出∠D的度数.
解答: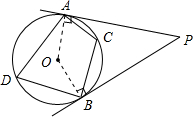 解:连接OA、OB.
解:连接OA、OB.
∵PA,PB分别切⊙O于点A,B,
∴OA⊥PA,OB⊥PB;
∴∠PAO=∠PBO=90°;
又∵∠APB=50°,
∴在四边形AOBP中,∠AOB=360°-90°-90°-50°=130°,
∴∠ADB=
×∠AOB=
×130°=65°,
即当C在D处时,∠ACB=65°.
在四边形ADBC中,∠ACB=180°-∠ADB=180°-65°=115°.
于是∠ACB的度数为65°或115°.
 解:连接OA、OB.
解:连接OA、OB.∵PA,PB分别切⊙O于点A,B,
∴OA⊥PA,OB⊥PB;
∴∠PAO=∠PBO=90°;
又∵∠APB=50°,
∴在四边形AOBP中,∠AOB=360°-90°-90°-50°=130°,
∴∠ADB=
| 1 |
| 2 |
| 1 |
| 2 |
即当C在D处时,∠ACB=65°.
在四边形ADBC中,∠ACB=180°-∠ADB=180°-65°=115°.
于是∠ACB的度数为65°或115°.
点评:本题考查的是切线的性质定理,圆内接四边形的性质,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知P为⊙O外一点,PA,PB为⊙O的切线,A、B为切点,∠P=70°,C为⊙O上一个动点,且不与A、B重合,则∠BCA=( )
| A、35°、145° | B、110°、70° | C、55°、125° | D、110° |
 已知,如图,点P为⊙O外一点,PA与⊙O相切于A点,B为⊙O上一点,PA=PB=
已知,如图,点P为⊙O外一点,PA与⊙O相切于A点,B为⊙O上一点,PA=PB=