题目内容
问题.你能很快算出20152的值吗?
为了解决这个问题,我们要观察个位上的数字是5的自然数的平方.任意一个个位数字为5的自然数可写成10n+5,即求(10n+5)2的值(n为自然数).你试分析n=1,n=2,n=3,…,这些简单情况,从中探索规律,并归纳猜想出结论(在下面空格内填上你的探索结果)
(1)通过计算,探索规律:
152=225可写成100×1×(1+1)+25,
252=625可写成100×2×(2+1)+25,
352=1225可写成100×3×(3+1)+25,
…
752=5625可写成
852=7225可写成
(2)依据(1)的结果,归纳猜想得(10n+5)2= ;
(3)根据上面的归纳、猜想,请你算出20152= .
为了解决这个问题,我们要观察个位上的数字是5的自然数的平方.任意一个个位数字为5的自然数可写成10n+5,即求(10n+5)2的值(n为自然数).你试分析n=1,n=2,n=3,…,这些简单情况,从中探索规律,并归纳猜想出结论(在下面空格内填上你的探索结果)
(1)通过计算,探索规律:
152=225可写成100×1×(1+1)+25,
252=625可写成100×2×(2+1)+25,
352=1225可写成100×3×(3+1)+25,
…
752=5625可写成
852=7225可写成
(2)依据(1)的结果,归纳猜想得(10n+5)2=
(3)根据上面的归纳、猜想,请你算出20152=
考点:完全平方公式,规律型:数字的变化类
专题:
分析:(1)先认真审题,观察已知中算式的计算过程,根据计算过程得出规律,即可得出答案;
(2)根据计算过程得出规律,即可得出答案;
(3)根据计算过程得出规律,即可得出答案.
(2)根据计算过程得出规律,即可得出答案;
(3)根据计算过程得出规律,即可得出答案.
解答:解:(1)通过计算,探索规律:
∵152=225可写成100×1×(1+1)+25,252=625可写成100×2×(2+1)+25,
352=1225可写成100×3×(3+1)+25,…
∴752=5625可写成 100×7×(7+1)+25,
852=7225可写成100×8×(8+1)+25,
故答案为:100×7×(7+1)+25,100×8×(8+1)+25;
(2)依据(1)的结果,归纳猜想得(10n+5)2=100n(n+1)+25,
故答案为100n(n+1)+25;
(3)根据上面的归纳、猜想,请你算出20152=100×201×(201+1)+25=4060225,
故答案为:100×201×(201+1)+25=4060225.
∵152=225可写成100×1×(1+1)+25,252=625可写成100×2×(2+1)+25,
352=1225可写成100×3×(3+1)+25,…
∴752=5625可写成 100×7×(7+1)+25,
852=7225可写成100×8×(8+1)+25,
故答案为:100×7×(7+1)+25,100×8×(8+1)+25;
(2)依据(1)的结果,归纳猜想得(10n+5)2=100n(n+1)+25,
故答案为100n(n+1)+25;
(3)根据上面的归纳、猜想,请你算出20152=100×201×(201+1)+25=4060225,
故答案为:100×201×(201+1)+25=4060225.
点评:本考查了完全平方公式的应用,解此题的关键是能根据求出的结果和算式得出规律,题目比较好,有一定的难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,为得到△DEF,需将△ABC( )
如图,为得到△DEF,需将△ABC( )| A、向左平移4个单位,再向下平移2个单位 |
| B、向右平移4个单位,再向下平移2个单位 |
| C、向右平移4个单位,再向上平移2个单位 |
| D、向左平移4个单位,再向上平移2个单位 |
下列命题中,是真命题的是( )
| A、相等的两个角是对顶角 |
| B、有公共顶点的两个角是对顶角 |
| C、一条直线只有一条垂线 |
| D、过直线外一点有且只有一条直线垂直于已知直线 |
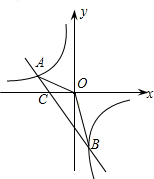 如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=
如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=