题目内容
15.△ABC中,∠A:∠B:∠C=1:2:3,最小边BC=4cm,则最长边AB的长是( )| A. | 5cm | B. | 6cm | C. | $\sqrt{5}$cm | D. | 8cm |
分析 利用三角形的内角和和角的比求出三边的比,再由最小边BC=4cm,即可求出最长边AB的长.
解答 解:设∠A=x,
则∠B=2x,∠C=3x,
由三角形内角和定理得∠A+∠B+∠C=x+2x+3x=180°
解得x=30°
即∠A=30°,∠C=3×30°=90°
此三角形为直角三角形
故AB=2BC=2×4=8cm
故选D.
点评 本题考查的是含30度角的直角三角形的性质,即在直角三角形中30°的角所对的边等于斜边的一半.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
3.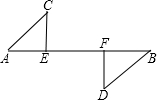 如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )
如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )
 如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )
如图,CE⊥AB,DF⊥AB,垂足分别为E、F,AC∥DB,且AC=BD,那么Rt△AEC≌Rt△BFD的理由是( )| A. | SSS | B. | AAS | C. | SAS | D. | HL |
20.计算5+(-5)=( )
| A. | 1 | B. | 0 | C. | 10 | D. | -10 |
4.下列图案中,是轴对称图形且有两条对称轴的是( )
| A. |  | B. |  | C. |  | D. |  |
5.下列计算结果正确的是( )
| A. | -(2x-y)=-2x-y | B. | -3a+(4a2+2)=-3a+4a2-2 | ||
| C. | -(2a-3y)=-2a+3y | D. | -3(a-7)=-3a+7 |
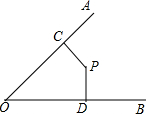 数学课上,老师要求学生证明:“到角的两边距离相等的点在这个角的平分线上”,请你结合图形书写已知、求证,并完成证明过程:
数学课上,老师要求学生证明:“到角的两边距离相等的点在这个角的平分线上”,请你结合图形书写已知、求证,并完成证明过程: