题目内容
20．下列条件中，不能得到等边三角形的是（ ）| A． | 有两个内角是60°的三角形 | |
| B． | 有两边相等且是轴对称图形的三角形 | |
| C． | 三边都相等的三角形 | |
| D． | 有一个角是60°且是轴对称图形的三角形 |
分析 根据等边三角形的定义可知：满足三边相等、有一内角为60°且两边相等或有两个内角为60°中任意一个条件的三角形都是等边三角形．
解答 解：A、两个内角为60°，根据三角形的内角和为180°，可知另一个内角也为60°，所以该三角形为等边三角形．故不符合题意；
B、两边相等说明是等腰三角形或等边三角形，而这两种三角形都满足“轴对称”的条件，所以不能确定该三角形是等边三角形．故符合题意；
C、三边都相等的三角形当然是等边三角形．故不符合题意；
D、“轴对称”说明该三角形有两边相等，且有一个角是60°，有两边相等且一角为60°的三角形是等边三角形．故不符合题意；
故选B．
点评 此题主要考查了等边三角形的判定，轴对称图形的定义，掌握等边三角形的判定是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，圆O的半径为2$\sqrt{2}$，AB、AC是圆O的两条弦，AB=2$\sqrt{3}$，AC=4，如果以O为圆心，作一个与AC相切的圆，那么这个圆的半径是多少？它与AB又怎样的位置关系？为什么？
8．
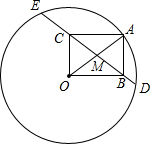如图，⊙O的半径为10，A是⊙O上一点．以OA为对角线作矩形OBAC，且OC=6．延长BC，与⊙O分别交于D，E两点，则△OCE和△OBD的周长差等于（ ）
如图，⊙O的半径为10，A是⊙O上一点．以OA为对角线作矩形OBAC，且OC=6．延长BC，与⊙O分别交于D，E两点，则△OCE和△OBD的周长差等于（ ）| A． | $\frac{3}{5}$ | B． | $\frac{4}{5}$ | C． | 1 | D． | $\frac{6}{5}$ |
5．
如图，PA，PB分别切⊙O于A，B，∠APB=60°，PA=8，则⊙O的半径OA长为（ ）
如图，PA，PB分别切⊙O于A，B，∠APB=60°，PA=8，则⊙O的半径OA长为（ ）| A． | 4 | B． | 8 | C． | $\frac{4}{3}$$\sqrt{3}$ | D． | $\frac{8}{3}$$\sqrt{3}$ |
12．
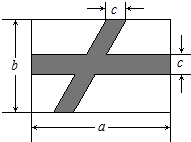如图所示，在公园长方形空地上，要修两条路（图中的阴影所示），按照图中标的数据，计算图中空白部分的面积为（ ）
如图所示，在公园长方形空地上，要修两条路（图中的阴影所示），按照图中标的数据，计算图中空白部分的面积为（ ）| A． | ab-bc-ac+c2 | B． | bc-ab+ac | C． | b2-bc+a2-ab | D． | a2+ab+bc-ac |
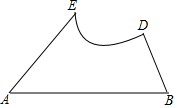有一个三角形工件△ABC，根据安装需要，把∠C切掉了，如图，现在要在工件上画出一条线段，使它是∠C的平分线在阴影面留下的那部分．