题目内容
8.如图,在Rt△ABC中,∠BAC=90°,AB=AC,在BC的同侧作任意Rt△DBC,∠BDC=90°.(1)若CD=2BD,M是CD中点(如图1),求证:△ADB≌△AMC;

下面是小明的证明过程,请你将它补充完整:
证明:设AB与CD相交于点O,
∵∠BDC=90°,∠BAC=90°,
∴∠DOB+∠DBO=∠AOC+∠ACO=90°.
∵∠DOB=∠AOC,
∴∠DBO=∠MCA
∵M是DC的中点,
∴CM=$\frac{1}{2}$CD=BD
又∵AB=AC,
∴△ADB≌△AMC.
(2)若CD<BD(如图2),在BD上是否存在一点N,使得△ADN是以DN为斜边的等腰直角三角形?若存在,请在图2中确定点N的位置,并加以证明;若不存在,请说明理由;
(3)当CD≠BD时,线段AD,BD与CD满足怎样的数量关系?请直接写出.
分析 (1)根据直角三角形的性质和中点的性质就可以的得出结论;
(2)存在.在BD上截取BN=CD,由条件可以得出,△ACD≌△ABN,就有AN=AD,∠DAC=∠NAB,得出∠NAD=90°而得出结论;
(3)当BD>CD时,如图3,在BD上截取BN=CD,由条件可以得出,△ACD≌△ABN,就有AN=AD,∠DAC=∠NAB,得出△AND是等腰直角三角形,就可以得出ND=$\sqrt{2}$AD,就可以得出BD-CD=$\sqrt{2}$.当BD<CD事实,如图4,在CD上取一点N,使CN=BD,由条件可以得出,△ACN≌△ABD,就有AN=AD,∠DAB=∠NAC,得出△AND是等腰直角三角形,就可以得出ND=$\sqrt{2}$AD,就可以得出CD-BD=$\sqrt{2}$.
解答 解:(1)由题意,得
①根据直角三角形的性质就可以得出:∠DBO=∠MCA(或∠ACO);
②由等式的性质就可以得出CM=BD;
故答案为:MCA,BD;
(2)存在.
理由:如图3,在BD上截取BN=CD,
∵∠BAC=∠BDC=90°,∠AOB=∠COD,
∴∠ABN=∠ACD.
在△ACD和△ABN中,
$\left\{\begin{array}{l}{AC=AB}\\{∠ACD=∠ABN}\\{CD=BN}\end{array}\right.$,
∴△ACD≌△ABN(SAS),
∴AN=AD,∠DAC=∠NAB.
∵∠NAB+∠NAC=90°,
∴∠DAC+∠NAC=90°,
即∠NAD=90°,
∴△NAD为等腰直角三角形;
(3)①当CD<BD时,$\sqrt{2}$AD=BD-CD.
理由:如图3,在BD上截取BN=CD,
∵∠BAC=∠BDC=90°,∠AOB=∠COD,
∴∠ABN=∠ACD.
在△ACD和△ABN中,
$\left\{\begin{array}{l}{AC=AB}\\{∠ACD=∠ABN}\\{CD=BN}\end{array}\right.$,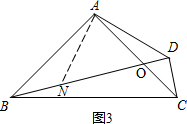
∴△ACD≌△ABN(SAS),
∴AN=AD,∠DAC=∠NAB.
∵∠NAB+∠NAC=90°,
∴∠DAC+∠NAC=90°,
即∠NAD=90°,
∴△NAD为等腰直角三角形;
∴ND=$\sqrt{2}$AD.
∵ND=BD-BN,
∴ND=BD-CD,
∴$\sqrt{2}$AD=BD-CD;
②当CD>BD时,$\sqrt{2}$AD=CD-BD;
理由:如图4,在CD上取一点N,使CN=BD,
∵∠BAC=∠BDC=90°,∠DOB=∠COA,
∴∠ABD=∠ACD.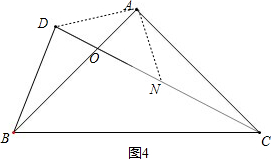
在△ACN和△ABD中,
$\left\{\begin{array}{l}{AC=AB}\\{∠ACN=∠ABD}\\{CN=BD}\end{array}\right.$,
∴△ACN≌△ABD(SAS),
∴AN=AD,∠DAB=∠NAC.
∵∠NAB+∠NAC=90°,
∴∠DAB+∠NAC=90°,
即∠NAD=90°,
∴△NAD为等腰直角三角形,
∴DN=$\sqrt{2}$AD.
∵DN=CD-CN,
∴DN=CD-BD,
∴$\sqrt{2}$AD=CD-BD.
点评 本题考查了等腰直角三角形的判定与性质的运用,全等三角形的判定与性质的运用,直角三角形的性质的运用,勾股定理的运用,解答时证明三角形全等是关键.

| A. | x>3 | B. | x>3或x<-3 | C. | x≧3 | D. | x≧-3 |
| A. | 任何实数都有相反数、倒数 | |
| B. | 过一点有且只有一条直线与已知直线平行 | |
| C. | 在同一平面内不相交的两条直线叫做平行线 | |
| D. | 两条直线被第三条直线所截,同位角相等 |
| A. |  | B. |  | C. |  | D. |  |
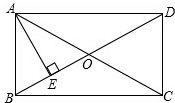 在矩形ABCD中,对角线AC、BD交于点O,AE⊥BD,垂足为E,且AE平分∠BAO.若DO=2,求AB和BC的长度.
在矩形ABCD中,对角线AC、BD交于点O,AE⊥BD,垂足为E,且AE平分∠BAO.若DO=2,求AB和BC的长度.