Question

【题目】若抛物线(是常数，)与直线都经过轴上的一点，且抛物线的顶点在直线上，则称此直线与该抛物线具有“一带一路”关系．此时，直线叫做抛物线的“带线”，抛物线叫做直线的“路线”．

（1）若直线与抛物线具有“一带一路”关系，求的值；

（2）若某“路线”的顶点在反比例函数的图象上，它的“带线”的解析式为，求此“路线”的解析式；

（3）当常数满足时，请直接写出抛物线：的“带线”与轴，轴所围成的三角形面积S的取值范围．

Answer 1

【答案】（1）p的值为-1，q的值为2；（2）y=x2+2x-1或y= x2+2x-1；（3）≤S≤．

【解析】

（1）由直线解析式可求出直线与y轴的交点坐标，代入可求出q值，根据抛物线解析式可求出顶点坐标，代入即可求出p值；

（2）根据“带线”解析式可得出直线与y轴的交点坐标为（0，-1），联立“带线”与反比例函数解析式可求出抛物线的顶点坐标为（2，1）或（-1，-2），根据二次函数顶点坐标分别设出解析式，把（0，-1）分别代入即可得答案；

（3）由抛物线解析式可得出抛物线与y轴的交点坐标为（0，k），根据抛物线的解析式可用k表示出其顶点坐标，由两点坐标结合待定系数法即可得出与该抛物线对应的“带线”l的解析式，找出该直线与x、y轴的交点坐标，结合三角形的面积得出面积S关于k的关系式，由二次函数的性质即可得出结论．

（1）令直线y=px+2中x=0，

∴y=2，

∴直线与y轴的交点为（0，2）；

∵直线与抛物线具有“一带一路”关系，

∴y=x2-2x+q的图象经过点（0，2），

∴把（0，2）代入y=x2-2x+q得：q=2，

∴抛物线的解析式为y=x2-2x+2=（x-1）2+1，

∴抛物线的顶点坐标为（1，1），

∵直线y=px+2经过抛物线y=x2-2x+q的顶点，

∴1=P+2，

解得：p=-1．

答：p的值为-1，q的值为2．

（2）令“带线”：中x=0得：y=-1，

∴“带线”与y轴的交点坐标为（0，-1），

联立“带线”与反比例函数解析式得：，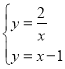

解得：，，

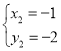∴抛物线的顶点坐标为（2，1）或（-1，-2），

当顶点坐标为（2，1）时，设“路线”的解析式为y=a(x-2)2+1，

把（0，-1）代入得：-1=4a+1，

解得：a=，

∴“路线”的解析式为y=（x-2）2+1=x2+2x-1，

当顶点坐标为（-1，-2）时，设“路线”的解析式为y=a(x+1)2-2，

把（0，-1）代入得：-1=a-2，

解得：a=1，

∴“路线”的解析式为y=(x+1)2-2=x2+2x-1，

综上所述：“路线”的解析式为y=x2+2x-1或y= x2+2x-1．

（3）令抛物线：中x=0得：y=k，

∴该抛物线与y轴的交点为（0，k），

∵抛物线的解析式为，

∴顶点坐标为[，]，

设“带线”的解析式为y=mx+k，

∵点[，]在y=mx+k图象上，

∴=m[]+k，

解得：m=，

∴“带线”的解析式为y=x+k，

令“带线”：y=x+k中y=0得：x+k=0，

解得：x=，

∴“带线”与x轴得交点为（，0），与y轴交点坐标为（0，k），

∴S=|||k|，

∵，

∴，

∴，

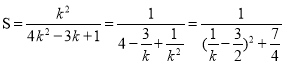∴当时，S有最大值为，

∵||＜|-4|，

∴当时，时，取最大值，

∴时，S有最小值，

∴S的取值范围为≤S≤．