题目内容
17. 如图,矩形EFGH内接于△ABC,AD⊥BC于点D,交EH于点M,若BC=8cm,AD=8cm,EH=3EF,EH=$\frac{72}{13}$cm.
如图,矩形EFGH内接于△ABC,AD⊥BC于点D,交EH于点M,若BC=8cm,AD=8cm,EH=3EF,EH=$\frac{72}{13}$cm.
分析 设EF=x,利用三角形相似的性质:对应边成比例,可求出x,进而求出EH的.
解答 解:设EF=x,则HE=3x
∵矩形EFGH内接于△ABC且AD⊥BC
∴EH∥BC,EF∥AD
∴△AEH∽△ABC,△BFE∽△BDA,
∴$\frac{HE}{BC}=\frac{AE}{AB}$,$\frac{EF}{AD}=\frac{BE}{AB}$,
∴$\frac{3x}{8}=\frac{AE}{AB}$,$\frac{x}{8}=\frac{BE}{AE}$,
∴$\frac{3x}{8}$+$\frac{x}{6}$=$\frac{AE}{AB}+\frac{BE}{AB}=1$,
∴x=$\frac{24}{13}$,
∴EH=3x=$\frac{72}{13}$cm,
故答案为$\frac{72}{13}$.
点评 本题考查了相似三角形的性质和判定,对于三角形相似类型的题目求边长,周长等,常常要用相似三角形的对应边成比例的性质来解题,这是常识,应记住并应用

练习册系列答案
相关题目
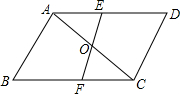 如图:AB∥CD且AB=CD,过AC中点O的直线分别交AD、BC于点E,F,则BF=DE吗?说明理由.
如图:AB∥CD且AB=CD,过AC中点O的直线分别交AD、BC于点E,F,则BF=DE吗?说明理由.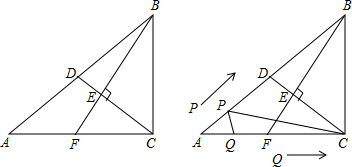 如图,Rt△ABC中,∠ACB=90°,BC=6,AC=8.D是斜边AB的中点,BF⊥CD于点E,交AC于点F.
如图,Rt△ABC中,∠ACB=90°,BC=6,AC=8.D是斜边AB的中点,BF⊥CD于点E,交AC于点F.