题目内容
已知一条抛物线的形状与开口方向都与抛物线y=-x2相同,它的顶点在直线y=2x+1上,且经过这条直线与x轴的交点,求这条抛物线的解析式.
考点:待定系数法求二次函数解析式
专题:计算题
分析:根据题意设抛物线解析式为y=-(x-m)2+2m+1,求出直线y=2x+1与x轴的交点,代入计算求出m的值,即可确定出抛物线解析式.
解答:解:根据题意设抛物线解析式为y=-(x-m)2+2m+1,
对于直线y=2x+1,令y=0,得到x=-
,
把x=-
,y=0代入得:0=-(
+m)2+2m+1,
解得:m=
或m=-
,
则这条抛物线解析式为y=-(x-
)2+4=-x2+3x+
或y=-(x+
)2=-x2-x-
.
对于直线y=2x+1,令y=0,得到x=-
| 1 |
| 2 |
把x=-
| 1 |
| 2 |
| 1 |
| 2 |
解得:m=
| 3 |
| 2 |
| 1 |
| 2 |
则这条抛物线解析式为y=-(x-
| 3 |
| 2 |
| 7 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
点评:此题考查了待定系数法求二次函数解析式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
一个扇形的周长为8m,则它的最大面积是( )
| A、4m2 |
| B、6m2 |
| C、8m2 |
| D、10m2 |
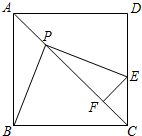 已知边长为1的正方形ABCD中, P是对角线AC上的一个动点(与点A、C不重合),过点P作PE⊥PB ,PE交射线DC于点E,过点E作EF⊥AC,垂足为点F.
已知边长为1的正方形ABCD中, P是对角线AC上的一个动点(与点A、C不重合),过点P作PE⊥PB ,PE交射线DC于点E,过点E作EF⊥AC,垂足为点F.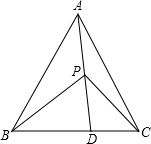 如图所示,在△ABC中,AB=AC,BD=2DC,P在AD上,∠BAC=∠BPD,求证:∠BPD=2∠CPD.
如图所示,在△ABC中,AB=AC,BD=2DC,P在AD上,∠BAC=∠BPD,求证:∠BPD=2∠CPD. 如图,二次函数y在y=-
如图,二次函数y在y=-