题目内容
 如图,BO、CO分别为∠ABC、∠ACB的外角平分线,且∠BOC=60°,则∠A=
如图,BO、CO分别为∠ABC、∠ACB的外角平分线,且∠BOC=60°,则∠A=考点:三角形内角和定理
专题:
分析:根据三角形的一个外角等于与它不相邻的两个内角的和和角平分线的定义表示出∠OBC+∠OCB,再根据三角形的内角和定理求解即可.
解答:解:∵BO、CO分别为∠ABC、∠ACB的外角平分线,
∴∠OBC+∠OCB=
(∠ACB+∠A)+
(∠ABC+∠A)=
(∠ACB+∠A+∠ABC+∠他A),
在△ABC中,∠ACB+∠A+∠ABC=180°,
∴∠OBC+∠OCB=90°+
∠A,
在△OBC中,∠OBC+∠OCB+∠BOC=180°,
∴90°+
∠A+60°=180°,
解得∠A=60°.
故答案为:60°.
∴∠OBC+∠OCB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
在△ABC中,∠ACB+∠A+∠ABC=180°,
∴∠OBC+∠OCB=90°+
| 1 |
| 2 |
在△OBC中,∠OBC+∠OCB+∠BOC=180°,
∴90°+
| 1 |
| 2 |
解得∠A=60°.
故答案为:60°.
点评:本题考查了三角形内角和定理,角平分线的定义,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并准确识图理清各角度之间的关系是解题的关键,要注意整体思想的利用.

练习册系列答案
相关题目
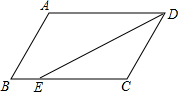 已知如图:?ABCD中,AD=8,AB=6,DE平分∠ADC交BC于E,则BE=
已知如图:?ABCD中,AD=8,AB=6,DE平分∠ADC交BC于E,则BE= 如图:两点A、B在直线MN外的同侧,AB=5,A到MN的距离AC=8,B到MN的距离BD=5,P在直线MN上运动,则|PA-PB|的最大值等于
如图:两点A、B在直线MN外的同侧,AB=5,A到MN的距离AC=8,B到MN的距离BD=5,P在直线MN上运动,则|PA-PB|的最大值等于