题目内容
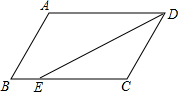已知如图：?ABCD中，AD=8，AB=6，DE平分∠ADC交BC于E，则BE=考点：平行四边形的性质
专题：
分析：根据角平分线的定义以及两直线平行，内错角相等求出∠CDE=∠CED，再根据等角对等边的性质可得CE=CD，然后利用平行四边形对边相等求出CD、BC的长度，再根据BE=BC-CE，代入数据计算即可得解．
解答：解：∵DE平分∠ADC，
∴∠ADE=∠CDE，
∵?ABCD中AD∥BC，
∴∠ADE=∠CED，
∴∠CDE=∠CED，
∴CE=CD，
∵在?ABCD中，AB=6，AD=8，
∴CD=AB=6，BC=AD=8，
∴BE=BC-CE=8-6=2．
故答案为：2．
∴∠ADE=∠CDE，
∵?ABCD中AD∥BC，
∴∠ADE=∠CED，
∴∠CDE=∠CED，
∴CE=CD，
∵在?ABCD中，AB=6，AD=8，
∴CD=AB=6，BC=AD=8，
∴BE=BC-CE=8-6=2．
故答案为：2．
点评：本题考查了平行四边形对边平行，对边相等的性质，角平分线的定义，等角对等边的性质，是基础题，准确识图并熟练掌握性质是解题的关键．
练习册系列答案
相关题目
如图，BO、CO分别为∠ABC、∠ACB的外角平分线，且∠BOC=60°，则∠A=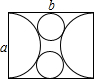
如图，用邻边长为a，b（a＜b）的矩形硬纸板截出以a为直径的两个半圆，再截出与矩形的较长边、两个半圆均相切的两个小圆，把半圆作为圆锥形圣诞帽的侧面，小圆恰好能作为底面，从而做成两个圣诞帽（拼接处材料忽略不计），则a与b关系式是
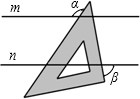小明同学把一个含有45°角的直角三角板放在如图的两条平行线m，n上，测得∠α=120°，则∠β的度数是