题目内容
14.等腰梯形上、下底长分别为2cm和6cm,且两条对角线互相垂直,则这个梯形的面积为16cm2.分析 如图,梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,AD=2cm,BC=6cm,根据等腰梯形的对称性,过O点作梯形对称轴EF,交AD于E,交BC于F,可证△AOD,△BOC为等腰直角三角形,得到OE=$\frac{1}{2}$AD=1,OF=$\frac{1}{2}$BC=3,可得梯形的高,从而计算梯形面积
解答 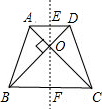 解:过O点作梯形对称轴EF,交AD于E,交BC于F,
解:过O点作梯形对称轴EF,交AD于E,交BC于F,
根据等腰梯形的对称性可知,OA=OD,OB=OC,
又∵AC⊥BD,
∴△AOD,△BOC为等腰直角三角形,
∴OE=$\frac{1}{2}$AD=1,OF=$\frac{1}{2}$BC=3,EF=OE+OF=4,
∴S梯形ABCD=$\frac{1}{2}$×EF×(AD+BC)=$\frac{1}{2}$×4×(2+6)=16cm2.
故答案为:16.
点评 本题考查了等腰梯形的轴对称性,等腰直角三角形的性质.关键是求出等腰梯形的高EF.本题也可以平移一腰,即过D点作AC的平行线交BC的延长线于G点,则有S梯形ABCD=S△DBG.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
9.为了加强公民的节水意识,合理利用水资源,某市采用价格调控手段达到节水目的,该市自来水收费价目表,如图所示,
(1)若该用户1月用水9m3,则应收水费24元;
(2)若该用户2月缴水费48元;求该用户2月用多少立方米的水?
(3)若该户居民3、4月份共用水15m3(4月份用水量超过3月份),共交水费44元,则该居民3、4各月份用水多少立方米?
| 价目表 | |
| 每月用水量 | 单价 |
| 不超出6m3的部分 | 2元/m3 |
| 超出6m3不超出10m3的部分 | 4元/m3 |
| 超出10m3的部分 | 8元/m3 |
| 注:消费按月结算 | |
(2)若该用户2月缴水费48元;求该用户2月用多少立方米的水?
(3)若该户居民3、4月份共用水15m3(4月份用水量超过3月份),共交水费44元,则该居民3、4各月份用水多少立方米?