题目内容
【题目】已知在平面直角坐标系![]() 中,直线
中,直线![]() 分别交
分别交![]() 轴和
轴和![]() 轴于点
轴于点![]() .
.
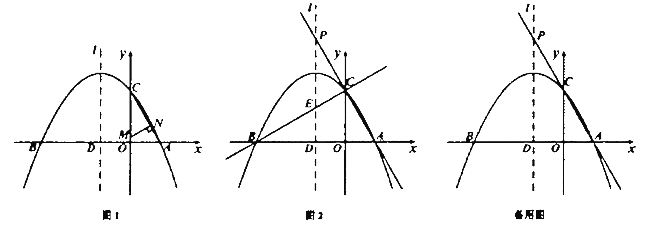
(1)如图1,已知![]() 经过点
经过点![]() ,且与直线
,且与直线![]() 相切于点
相切于点![]() ,求
,求![]() 的直径长;
的直径长;
(2)如图2,已知直线![]() 分别交
分别交![]() 轴和
轴和![]() 轴于点
轴于点![]() 和点
和点![]() ,点
,点![]() 是直线
是直线![]() 上的一个动点,以
上的一个动点,以![]() 为圆心,
为圆心,![]() 为半径画圆.
为半径画圆.
①当点![]() 与点
与点![]() 重合时,求证: 直线
重合时,求证: 直线![]() 与
与![]() 相切;
相切;
②设![]() 与直线
与直线![]() 相交于
相交于![]() 两点, 连结
两点, 连结![]() . 问:是否存在这样的点
. 问:是否存在这样的点![]() ,使得
,使得![]() 是等腰直角三角形,若存在,求出点
是等腰直角三角形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
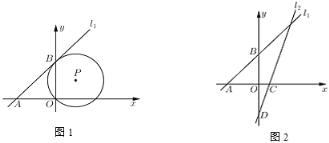
【答案】(1) ![]() 的直径长为
的直径长为![]() ;(2) ①见解析;②存在这样的点
;(2) ①见解析;②存在这样的点![]() 和
和![]() ,使得
,使得![]() 是等腰直角三角形.
是等腰直角三角形.
【解析】
(1)连接BC,证明△ABC为等腰直角三角形,则⊙P的直径长=BC=AB,即可求解;
(2)过点![]() 作
作![]() 于点
于点![]() ,证明CE=ACsin45°=4×
,证明CE=ACsin45°=4×![]() =2
=2![]() =圆的半径,即可求解;
=圆的半径,即可求解;
(3)假设存在这样的点![]() ,使得
,使得![]() 是等腰直角三角形,分点
是等腰直角三角形,分点![]() 在线段
在线段![]() 上时和点
上时和点![]() 在线段
在线段![]() 的延长线上两种情况,分别求解即可.
的延长线上两种情况,分别求解即可.
(1)如图3,连接BC,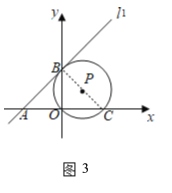
∵∠BOC=90°,
∴点P在BC上,
∵⊙P与直线l1相切于点B,
∴∠ABC=90°,而OA=OB,
∴△ABC为等腰直角三角形,
则⊙P的直径长=BC=AB=3![]()
(2)如图4过点![]() 作
作![]() 于点
于点![]() ,
,
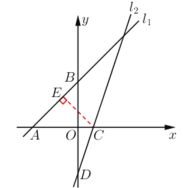
图4
将![]() 代入
代入![]() ,得
,得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
∵点![]() 与点
与点![]() 重合,
重合,
又![]() 的半径为
的半径为![]() ,
,
∴直线![]() 与
与![]() 相切.
相切.
②假设存在这样的点![]() ,使得
,使得![]() 是等腰直角三角形,
是等腰直角三角形,
∵直线![]() 经过点
经过点![]() ,
,
∴![]() 的函数解析式为
的函数解析式为![]() .
.
记直线![]() 与
与![]() 的交点为
的交点为![]() ,
,
情况一:
如图5,当点![]() 在线段
在线段![]() 上时,
上时,
由题意,得![]() .
.
如图,延长![]() 交
交![]() 轴于点
轴于点![]() ,
,
图5
∵![]() ,
,
∴![]() ,
,
即![]() 轴,
轴,
∴点![]() 与
与![]() 有相同的横坐标,
有相同的横坐标,
设![]() ,则
,则![]() ,
,
∴![]() .
.
∵![]() 的半径为
的半径为![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴![]() ,
,
∴![]() 的坐标为
的坐标为![]() .
.
情况二:
当点![]() 在线段
在线段![]() 的延长线上时,同理可得
的延长线上时,同理可得![]() ,
,![]() 的坐标为
的坐标为![]() .
.
∴存在这样的点![]() 和
和![]() ,使得
,使得![]() 是等腰直角三角形.
是等腰直角三角形.

练习册系列答案
相关题目