题目内容
在平面直角坐标系xOy中,点A的坐标为(3,2),若将线段OA绕点O顺时针旋转90°得到线段OA′,则点A′的坐标是 .
考点:坐标与图形变化-旋转
专题:
分析:作AB⊥y轴于B,A′B′⊥x轴于B′.根据A点坐标可知AB、OB长度,由旋转的性质知A′B′、OB′的长度,根据A′所在象限确定其坐标.
解答:解:作AB⊥y轴于B,A′B′⊥x轴于B′.
∵A(3,2),
∴AB=3,OB=2.
∴A′B′=3,OB′=2.
因为A′在第四象限,
∴A′(2,-3).
故答案为(2,-3).
∵A(3,2),
∴AB=3,OB=2.
∴A′B′=3,OB′=2.
因为A′在第四象限,
∴A′(2,-3).
故答案为(2,-3).
点评:考查了坐标与图形变化-旋转,需注意旋转前后对应线段的长度不变,确定坐标时注意点所在象限.

练习册系列答案
相关题目
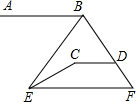 如图,AB∥CD∥EF,∠ABE=50°,∠ECD=160°,则∠BEC的度数为( )
如图,AB∥CD∥EF,∠ABE=50°,∠ECD=160°,则∠BEC的度数为( )| A、20° | B、25° |
| C、30° | D、35° |
若代数式
有意义,那么x的取值范围是( )
| ||
| x-2 |
| A、x>2 | B、x≥1 |
| C、x≥1且x≠2 | D、x≠2 |
 星期日,小明同学从家中出发,步行去菜地里浇水,浇完后又去玉米地里除草,然后回到家里.如图是所用的时间与离家的距离的关系的图象,若菜地和玉米地的距离为a千米,在玉米地里除草比在菜地里浇水多用的时间为b分钟,则a=
星期日,小明同学从家中出发,步行去菜地里浇水,浇完后又去玉米地里除草,然后回到家里.如图是所用的时间与离家的距离的关系的图象,若菜地和玉米地的距离为a千米,在玉米地里除草比在菜地里浇水多用的时间为b分钟,则a= 如图,在△ABC中,EF∥BC,∠ACG是△ABC的外角,∠BAC的平分线交BC于点D,记∠ADC=α,∠ACG=β,∠AEF=γ,则:α、β、γ三者间的数量关系式是
如图,在△ABC中,EF∥BC,∠ACG是△ABC的外角,∠BAC的平分线交BC于点D,记∠ADC=α,∠ACG=β,∠AEF=γ,则:α、β、γ三者间的数量关系式是 如图,点O是直线AD上一点,射线OC、OE分别是∠AOB、∠BOD的平分线,若∠AOC=25°,则∠BOE=
如图,点O是直线AD上一点,射线OC、OE分别是∠AOB、∠BOD的平分线,若∠AOC=25°,则∠BOE=