��Ŀ����
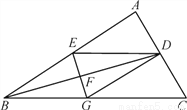
��ͼ��BD�ǡ�ABC�Ľ�ƽ���ߣ����Ĵ�ֱƽ���߷ֱ�AB��BD��BC�ڵ�E��F��G������ED��DG.
��1�����ж��ı���EBGD����״����˵�����ɣ�
��2������ABC��30�㣬��C��45�㣬ED��4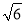 ����H��BD�ϵ�һ�����㣬��HG��HC����Сֵ��
����H��BD�ϵ�һ�����㣬��HG��HC����Сֵ��
��ϰ��ϵ�д�
 �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
�����Ŀ
��Ŀ����
��ͼ��BD�ǡ�ABC�Ľ�ƽ���ߣ����Ĵ�ֱƽ���߷ֱ�AB��BD��BC�ڵ�E��F��G������ED��DG.
��1�����ж��ı���EBGD����״����˵�����ɣ�
��2������ABC��30�㣬��C��45�㣬ED��4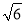 ����H��BD�ϵ�һ�����㣬��HG��HC����Сֵ��
����H��BD�ϵ�һ�����㣬��HG��HC����Сֵ��

 �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�