题目内容
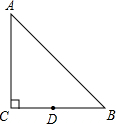如图，在△ABC中，AC=BC=2，∠ACB=90°，D是BC边上的中点，E是AB边上一动点，作出使EC+ED的值最小的点E．（不写作法，保留作图痕迹），此时EC+ED的最小值是多少？考点：轴对称-最短路线问题
专题：
分析：首先确定DC′=DE+EC′=DE+CE的值最小，然后根据勾股定理计算．
解答：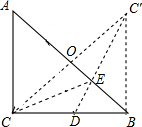
解：过点C作CO⊥AB于O，延长CO到C′，使OC′=OC，连接DC′，交AB于E，连接C′B，
此时DE+CE=DE+EC′=DC′的值最小．
连接BC′，由对称性可知∠C′BE=∠CBE=45°，
∴∠CBC′=90°，
∴BC′⊥BC，∠BCC′=∠BC′C=45°，
∴BC=BC′=2，
∵D是BC边的中点，
∴BD=1，
根据勾股定理可得：DC′=
=
=
，
故EC+ED的最小值是：
．
解：过点C作CO⊥AB于O，延长CO到C′，使OC′=OC，连接DC′，交AB于E，连接C′B，此时DE+CE=DE+EC′=DC′的值最小．
连接BC′，由对称性可知∠C′BE=∠CBE=45°，
∴∠CBC′=90°，
∴BC′⊥BC，∠BCC′=∠BC′C=45°，
∴BC=BC′=2，
∵D是BC边的中点，
∴BD=1，
根据勾股定理可得：DC′=
| BC′2+BD2 |
| 22+12 |
| 5 |
故EC+ED的最小值是：
| 5 |
点评：此题考查了轴对称求最短路线的问题，确定动点E何位置时，使EC+ED的值最小是关键．
练习册系列答案
相关题目
若|x-2|+（3y+2）2=0，则（x+1）y的值是（ ）
| A、-1 | ||
| B、-2 | ||
| C、-3 | ||
D、
|
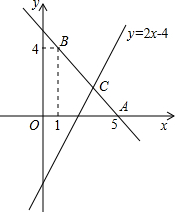如图，直线y=kx+b经过点A（0，5），B（1，4）．
如图，圆柱的高为10cm，底面半径为4cm，在圆柱下底面的B点处有一只蚂蚁，它想吃到上底面A 处的食物，蚂蚁爬行的最短路程是多少？（π取3）
已知某隧道截面拱形为抛物线形，拱顶离地面10米，底部宽20米．