题目内容
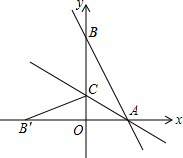 如图,直线y=-
如图,直线y=-| 12 |
| 5 |
考点:翻折变换(折叠问题),待定系数法求一次函数解析式
专题:
分析:由直线y=-
x+12与x轴、y轴分别交于A点和B点,可求得A与B的坐标,然后设OC=m,即可得方程82+m2=(12-m)2,解此方程即可求得点C的坐标,然后利用待定系数法即可求得直线AC的解析式.
| 12 |
| 5 |
解答:解:∵直线y=-
x+12与x轴、y轴分别交于A点和B点,
∴点A(5,0),点B(0,12),
∴AB=
=13,
设OC=m,
由折叠的性质:B′C=BC=OB-OC=12-m,OB′=AB′-OA=AB-OA=13-5=8,
在Rt△OB′C中,OB′2+OC2=B′C2,
∴82+m2=(12-m)2,
解得:m=
,
∴点C(0,
),
设直线AC的解析式为:y=kx+b,
∴
,
解得:
,
∴直线AC的解析式为:y=-
x+
.
故答案为:y=-
x+
.
| 12 |
| 5 |
∴点A(5,0),点B(0,12),
∴AB=
| 52+122 |
设OC=m,
由折叠的性质:B′C=BC=OB-OC=12-m,OB′=AB′-OA=AB-OA=13-5=8,
在Rt△OB′C中,OB′2+OC2=B′C2,
∴82+m2=(12-m)2,
解得:m=
| 10 |
| 3 |
∴点C(0,
| 10 |
| 3 |
设直线AC的解析式为:y=kx+b,
∴
|
解得:
|
∴直线AC的解析式为:y=-
| 2 |
| 3 |
| 10 |
| 3 |
故答案为:y=-
| 2 |
| 3 |
| 10 |
| 3 |
点评:此题考查了折叠的性质、待定系数法求一次函数的解析式以及勾股定理.此题难度适中,注意掌握折叠前后图形的对应关系,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下面式子中x和y成反比例的是( )
| A、x+y=60 | ||
B、
| ||
| C、x-y=60 | ||
| D、xy=60 |
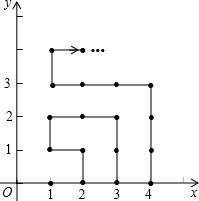 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1)(1,2),(2,2),…,根据这个规律,第2013个点的坐标为
如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排列,如(1,0),(2,0),(2,1),(1,1)(1,2),(2,2),…,根据这个规律,第2013个点的坐标为 在平面直角坐标系xOy中,过点A(6,5)作AB⊥x轴于点B.半径为r(0<r<5)的⊙A与AB交于点C,过B点作⊙A的切线BD,切点为D,连接DC并延长交x轴于点E.
在平面直角坐标系xOy中,过点A(6,5)作AB⊥x轴于点B.半径为r(0<r<5)的⊙A与AB交于点C,过B点作⊙A的切线BD,切点为D,连接DC并延长交x轴于点E.