题目内容
△ABC中,AD为BC上的中线,AB=1,AC=3,AD=
,则BC的长为 .
| 2 |
考点:全等三角形的判定与性质,勾股定理,勾股定理的逆定理
专题:
分析:作出图形,延长AD至E,使DE=AD,连接CE,利用“边角边”证明△ABD和△ECD全等,根据全等三角形对应边相等可得CE=AB,再利用勾股定理逆定理判断出△ACE是直角三角形,然后利用勾股定理列式求出CD,再根据BC=2CD计算即可得解.
解答: 解:如图,延长AD至E,使DE=AD,连接CE,
解:如图,延长AD至E,使DE=AD,连接CE,
∵AD为BC上的中线,
∴BD=CD,
在△ABD和△ECD中,
,
∴△ABD≌△ECD(SAS),
∴CE=AB=1,
∵AE2+CE2=(2
)2+12=8+1=9,
AC2=32=9,
∴AE2+CE2=AC2,
∴△ACE是直角三角形,∠E=90°,
由勾股定理得,CD=
=
=
,
∴BC=2CD=2
.
故答案为:2
.
 解:如图,延长AD至E,使DE=AD,连接CE,
解:如图,延长AD至E,使DE=AD,连接CE,∵AD为BC上的中线,
∴BD=CD,
在△ABD和△ECD中,
|
∴△ABD≌△ECD(SAS),
∴CE=AB=1,
∵AE2+CE2=(2
| 2 |
AC2=32=9,
∴AE2+CE2=AC2,
∴△ACE是直角三角形,∠E=90°,
由勾股定理得,CD=
| DE2+CE2 |
|
| 3 |
∴BC=2CD=2
| 3 |
故答案为:2
| 3 |
点评:本题考查了全等三角形的判定与性质,勾股定理逆定理,勾股定理,“遇中线加倍延”作辅助线构造出全等三角形是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
2014年3月3日是第15次全国爱耳日,主题为“爱耳护耳,健康听力--预防从初级耳科保健做起”.世界卫生组织2013年报告称,全球有3.6亿人有听力残疾,将数字3.6亿用科学记数法表示正确的是( )
| A、3.6×108 |
| B、0.36×109 |
| C、0.36×1011 |
| D、36×107 |
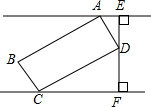 某单位为治理乱停车现象,出台了规范使用停车位的管理办法.如图,矩形ABCD是供一辆机动车停放的车位示意图,已知BC=2m,CD=5.6m,∠DCF=30°,请你计算车位所占的宽度EF为多少m?(结果保留根号)
某单位为治理乱停车现象,出台了规范使用停车位的管理办法.如图,矩形ABCD是供一辆机动车停放的车位示意图,已知BC=2m,CD=5.6m,∠DCF=30°,请你计算车位所占的宽度EF为多少m?(结果保留根号)
 如图,在△ABC中,DE是线段BC的垂直平分线,交BC于E,交AC于D.若AB=3,AC=7,则△ABD的周长是
如图,在△ABC中,DE是线段BC的垂直平分线,交BC于E,交AC于D.若AB=3,AC=7,则△ABD的周长是 如图,∠ACB=90°,CD⊥AB于D,AB=2BC,如果CD=2,则AC=
如图,∠ACB=90°,CD⊥AB于D,AB=2BC,如果CD=2,则AC=