Question

【题目】同一个圆的内接正方形和正三角形的边心距的比为_____．

Answer 1

【答案】

【解析】先画出同一个圆的内接正方形和内接正三角形，设⊙O的半径为R，求出正方形的边心距和正三角形的边心距，再求出比值即可．

设⊙O的半径为r，⊙O的内接正方形ABCD，如图，

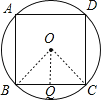
过O作OQ⊥BC于Q，连接OB、OC，即OQ为正方形ABCD的边心距，

∵四边形BACD是正方形，⊙O是正方形ABCD的外接圆，

∴O为正方形ABCD的中心，

∴∠BOC=90°，

∵OQ⊥BC，OB=CO，

∴QC=BQ，∠COQ=∠BOQ=45°，

∴OQ=OC×cos45°=R；

设⊙O的内接正△EFG，如图，

过O作OH⊥FG于H，连接OG，即OH为正△EFG的边心距，

∵正△EFG是⊙O的外接圆，

∴∠OGF=∠EGF=30°，

∴OH=OG×sin30°=R，

∴OQ：OH=（R）：（R）=：1，

故答案为：：1．