Question

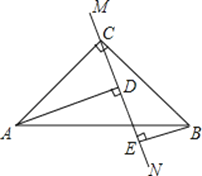
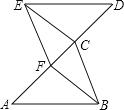
【题目】如图，已知A、F、C、D四点在同一条直线上，AF=CD，AB∥DE，且AB=DE．

（1）求证：△ABC≌△DEF；

（2）若EF=3，DE=4，∠DEF=90°，请直接写出使四边形EFBC为菱形时AF的长度．

Answer 1

【答案】（1）证明见解析；（2）AF=．

【解析】（1）根据SAS进行证明即可；

（2）利用勾股定理分别求出DF、OE、OF即可解决问题.

（1）∵AB∥DE，

∴∠A=∠D，

∵AF=CD，

∴AF+FC=CD+FC，

即AC=DF，

∵AB=DE，

∴△ABC≌△DEF；

（2）如图，连接AB交AD于O，

在Rt△EFD中，∵∠DEF=90°，EF=3，DE=4，

∴DF==5，

∵四边形EFBC是菱形，

∴BE⊥CF，∴EO=，

∴OF=OC=，

∴CF=，

∴AF=CD=DF﹣FC=5﹣=．