题目内容
18.若$\sqrt{3a+12}$与|b-$\sqrt{3}$|互为相反数,试解关于x的方程(2a+4)x2+b2+6=0.分析 根据非负数的性质得出a、b的值,再代入方程利用直接开平方法求解可得.
解答 解:∵$\sqrt{3a+12}$与|b-$\sqrt{3}$|互为相反数,
∴$\sqrt{3a+12}$+|b-$\sqrt{3}$|=0,
∴3a+12=0且b-$\sqrt{3}$=0,
解得:a=-4,b=$\sqrt{3}$,
则原方程可化为:-4x2+9=0,
∴x2=$\frac{9}{4}$,
解得:x=±$\frac{3}{2}$.
点评 本题主要考查非负数的性质和解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.

练习册系列答案
相关题目
9.原价为100元的某种药品经过连续两次降价后为64元,设平均每次降价的百分率为x,则下面所列方程正确的是( )
| A. | 100(1-x)2=64 | B. | 64(1-x)2=100 | C. | 100(1-2x)=64 | D. | 64(1-2x)=100 |
10.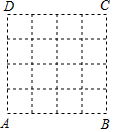 在数学活动课上,老师要求学生在4×4的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在各点上,而且三边与AB或AD都不平行,则画出的形状不同的直角三角形有( )种.
在数学活动课上,老师要求学生在4×4的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在各点上,而且三边与AB或AD都不平行,则画出的形状不同的直角三角形有( )种.
 在数学活动课上,老师要求学生在4×4的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在各点上,而且三边与AB或AD都不平行,则画出的形状不同的直角三角形有( )种.
在数学活动课上,老师要求学生在4×4的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在各点上,而且三边与AB或AD都不平行,则画出的形状不同的直角三角形有( )种.| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
1.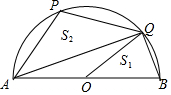 如图,在半圆O中,AB为直径,点P是圆上一点,连结AP,过O作OQ∥AP与半圆交于点Q,设△OQB的面积为S1,△APQ的面积为S2,若$\frac{{S}_{1}}{{S}_{2}}$=$\frac{5}{6}$,则tan∠PQA的值为( )
如图,在半圆O中,AB为直径,点P是圆上一点,连结AP,过O作OQ∥AP与半圆交于点Q,设△OQB的面积为S1,△APQ的面积为S2,若$\frac{{S}_{1}}{{S}_{2}}$=$\frac{5}{6}$,则tan∠PQA的值为( )
 如图,在半圆O中,AB为直径,点P是圆上一点,连结AP,过O作OQ∥AP与半圆交于点Q,设△OQB的面积为S1,△APQ的面积为S2,若$\frac{{S}_{1}}{{S}_{2}}$=$\frac{5}{6}$,则tan∠PQA的值为( )
如图,在半圆O中,AB为直径,点P是圆上一点,连结AP,过O作OQ∥AP与半圆交于点Q,设△OQB的面积为S1,△APQ的面积为S2,若$\frac{{S}_{1}}{{S}_{2}}$=$\frac{5}{6}$,则tan∠PQA的值为( )| A. | $\frac{5}{6}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
 已知y=-2x2+bx+c的图象经过点A(0,2)和B(-1,-4).
已知y=-2x2+bx+c的图象经过点A(0,2)和B(-1,-4).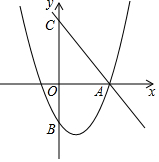 如图,直线y=-$\frac{4}{3}$x+4交x轴于点A,交y轴于点C,抛物线y=ax2-$\frac{4}{3}$x+c过点A,交y轴于点B(0,-2).
如图,直线y=-$\frac{4}{3}$x+4交x轴于点A,交y轴于点C,抛物线y=ax2-$\frac{4}{3}$x+c过点A,交y轴于点B(0,-2).
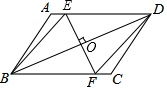 如图,在平行四边形ABCD中,点O是对角线BD的中点,过O点作EF⊥BD,交AD于E,交BC于F,那么,四边形EBFD是菱形吗?为什么?
如图,在平行四边形ABCD中,点O是对角线BD的中点,过O点作EF⊥BD,交AD于E,交BC于F,那么,四边形EBFD是菱形吗?为什么?