题目内容
16.如图1,△ABC和△DEF中,AB=AC,DE=DF,∠A=∠D.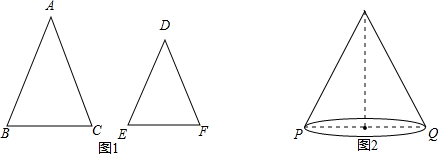
(1)求证:$\frac{BC}{AB}$=$\frac{EF}{DE}$;
(2)由(1)中的结论可知,等腰三角形ABC中,当顶角∠A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也就确定,我们把这个比值记作T(A),即T(A)=$\frac{∠A的对边(底边)}{∠A的邻边(腰)}$=$\frac{BC}{AB}$,如T(60°)=1.
①理解巩固:T(90°)=$\sqrt{2}$,T(120°)=$\sqrt{3}$,若α是等腰三角形的顶角,则T(α)的取值范围是0<T(α)<2;
②学以致用:如图2,圆锥的母线长为9,底面直径PQ=8,一只蚂蚁从点P沿着圆锥的侧面爬行到点Q,求蚂蚁爬行的最短路径长(精确到0.1).
(参考数据:T(160°)≈1.97,T(80°)≈1.29,T(40°)≈0.68)
分析 (1)证明△ABC∽△DEF,根据相似三角形的性质解答即可;
(2)①根据等腰直角三角形的性质和等腰三角形的性质进行计算即可;
②根据圆锥的侧面展开图的知识和扇形的弧长公式计算,得到扇形的圆心角,根据T(A)的定义解答即可.
解答 解:(1)∵AB=AC,DE=DF,
∴$\frac{AB}{DE}$=$\frac{AC}{DF}$,
又∵∠A=∠D,
∴△ABC∽△DEF,
∴$\frac{BC}{AB}$=$\frac{EF}{DE}$;
(2)①如图1,∠A=90°,AB=AC,
则$\frac{BC}{AB}$=$\sqrt{2}$,
∴T(90°)=$\sqrt{2}$, 如图2,∠A=120°,AB=AC,
如图2,∠A=120°,AB=AC,
作AD⊥BC于D,
则∠B=30°,
∴BD=$\frac{\sqrt{3}}{2}$AB,
∴BC=$\sqrt{3}$AB,
∴T(120°)=$\sqrt{3}$;
∵AB-AC<BC<AB+AC,
∴0<T(α)<2,
故答案为:$\sqrt{2}$;$\sqrt{3}$;0<T(α)<2;
②∵圆锥的底面直径PQ=8,
∴圆锥的底面周长为8π,即侧面展开图扇形的弧长为8π,
设扇形的圆心角为n°,
则$\frac{n×π×9}{180}$=8π,
解得,n=160,
∵T(80°)≈1.29,
∴蚂蚁爬行的最短路径长为1.29×9≈11.6.
点评 本题考查的是相似三角形的判定和性质、等腰三角形的性质以及T(A)的定义,正确理解T(A)的定义、掌握相似三角形的判定定理和性质定理是解题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
4. 某校为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
某校为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
参加社区活动次数的频数、频率分布表
根据以上图表信息,解答下列问题:
(1)表中a=12,b=0.08;
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
(3)若该校共有1200名学生,请估计该校在上学期参加社区活动超过6次的学生有多少人?
 某校为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:
某校为了解全校学生上学期参加社区活动的情况,学校随机调查了本校50名学生参加社区活动的次数,并将调查所得的数据整理如下:参加社区活动次数的频数、频率分布表
| 活动次数x | 频数 | 频率 |
| 0<x≤3 | 10 | 0.20 |
| 3<x≤6 | a | 0.24 |
| 6<x≤9 | 16 | 0.32 |
| 9<x≤12 | 6 | 0.12 |
| 12<x≤15 | m | b |
| 15<x≤18 | 2 | n |
(1)表中a=12,b=0.08;
(2)请把频数分布直方图补充完整(画图后请标注相应的数据);
(3)若该校共有1200名学生,请估计该校在上学期参加社区活动超过6次的学生有多少人?
11.已知M=$\frac{2}{9}$a-1,N=a2-$\frac{7}{9}$a(a为任意实数),则M、N的大小关系为( )
| A. | M<N | B. | M=N | C. | M>N | D. | 不能确定 |
1. 在Rt△ABC中,∠ACB=90°,AC=2$\sqrt{3}$,以点B为圆心,BC的长为半径作弧,交AB于点D,若点D为AB的中点,则阴影部分的面积是( )
在Rt△ABC中,∠ACB=90°,AC=2$\sqrt{3}$,以点B为圆心,BC的长为半径作弧,交AB于点D,若点D为AB的中点,则阴影部分的面积是( )
 在Rt△ABC中,∠ACB=90°,AC=2$\sqrt{3}$,以点B为圆心,BC的长为半径作弧,交AB于点D,若点D为AB的中点,则阴影部分的面积是( )
在Rt△ABC中,∠ACB=90°,AC=2$\sqrt{3}$,以点B为圆心,BC的长为半径作弧,交AB于点D,若点D为AB的中点,则阴影部分的面积是( )| A. | 2$\sqrt{3}$-$\frac{2}{3}$π | B. | 4$\sqrt{3}$-$\frac{2}{3}$π | C. | 2$\sqrt{3}$-$\frac{4}{3}$π | D. | $\frac{2}{3}$π |
6.-$\frac{1}{2016}$的相反数的倒数是( )
| A. | 1 | B. | -1 | C. | 2016 | D. | -2016 |
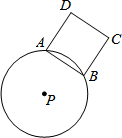 如图,⊙P的半径为5,A、B是圆上任意两点,且AB=6,以AB为边作正方形ABCD(点D、P在直线AB两侧).若AB边绕点P旋转一周,则CD边扫过的面积为9π.
如图,⊙P的半径为5,A、B是圆上任意两点,且AB=6,以AB为边作正方形ABCD(点D、P在直线AB两侧).若AB边绕点P旋转一周,则CD边扫过的面积为9π. 如图是由6个棱长均为1的正方体组成的几何体,它的主视图的面积为5.
如图是由6个棱长均为1的正方体组成的几何体,它的主视图的面积为5.