题目内容
12.已知⊙O的直径为4cm,A是圆上一固定点,弦BC的长为2$\sqrt{2}$cm(A、B、C三点均不重合),当△ABC为等腰三角形时,其底边上的高为2$+\sqrt{2}$或2,或2-$\sqrt{2}$.分析 当BC为底边时,如图1,连接AO延长与BC交于F,由全等三角形的判定定理得△ABO≌△ACO,∠BAO=∠CAO,得△AFB≌△ACF,由全等的性质得,BF=CF,由垂径定理得,AF⊥BC,AF为△ABC的高,利用勾股定理可得OF,可得AF的长;
当BC为腰时,如图2,连接BO并延长与AC交于F,由全等三角形的判定定理得△ABO≌△CBO,∠ABO=∠CBO,得△AFB≌△CBF,由全等的性质得,AF=CF,由垂径定理得,AF⊥AC,BF为△ABC的高,由勾股定理逆定理得,△BOC为等腰直角三角形,∠CBO=45°,由等腰三角形的性质得,BF=CF,利用勾股定理可得BF的长;
当如图3所示时,BC为底,利用垂径定理得BF=CF=$\sqrt{2}$,利用勾股定理可得AF的长.
解答 解:当BC为底边时,如图1,连接AO延长与BC交于F,
在△ABO与△ACO中,
$\left\{\begin{array}{l}{AB=AC}\\{BO=CO}\\{AO=AO}\end{array}\right.$,
∴△ABO≌△ACO(SSS),
∴∠BAO=∠CAO,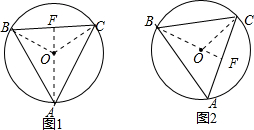
在△AFB与△ACF中,
$\left\{\begin{array}{l}{AF=AF}\\{∠BAO=∠CAO}\\{AB=AC}\end{array}\right.$,
∴△AFB≌△ACF(SAS),
∴BF=CF=$\sqrt{2}$,
∴AF⊥BC,
∴AF为△ABC的高,
在直角△BOF中,
OF=$\sqrt{B{O}^{2}-B{F}^{2}}$=$\sqrt{2}$,
∴AF=2+$\sqrt{2}$;
当BC为腰时,如图2,连接BO并延长与AC交于F
同理可证得:△ABO≌△CBO,
∴∠ABO=∠CBO,
可得△AFB≌△CBF,
∴AF=CF,
∴AF⊥AC,BF为△ABC的高,
∵OB2+OC2=8,BC2=8,
∴△BOC为等腰直角三角形,
∴∠CBO=45°,
∴CF=BF,
设CF=BF=x,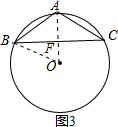
则2x2=8,
解得:x=2,
∴BF=2,
当如图3所示时,BC为底,
∵AF⊥BC,
∴BF=CF=$\sqrt{2}$,
设AF=x,则OF=2-x,
∴(2-x)2+($\sqrt{2}$)2=22,
解得:x=2+$\sqrt{2}$或x=2-$\sqrt{2}$
故答案为:2$+\sqrt{2}$或2,或2-$\sqrt{2}$.
点评 本题主要考查了等腰三角形的性质,垂径定理,勾股定理及其逆定理,分类讨论是解答此题的关键.

 名校课堂系列答案
名校课堂系列答案 如图,△OAB是由△ODC绕点O逆时针旋转30°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为110°,求∠DOB的度数.
如图,△OAB是由△ODC绕点O逆时针旋转30°后得到的图形,若点D恰好落在AB上,且∠AOC的度数为110°,求∠DOB的度数. 如图,△ABC≌△DEF,则∠A的对应角是∠D,BC与EF是对应边.
如图,△ABC≌△DEF,则∠A的对应角是∠D,BC与EF是对应边. 如图,菱形ABCD中,BP=CP,MN∥AB,求证:
如图,菱形ABCD中,BP=CP,MN∥AB,求证:
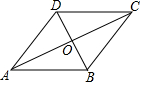 如图,?ABCD中,对角线AC,BD相交于点O,且AC⊥BD,请你添加一个适当的条件∠BAD=90°,使ABCD成为正方形.
如图,?ABCD中,对角线AC,BD相交于点O,且AC⊥BD,请你添加一个适当的条件∠BAD=90°,使ABCD成为正方形.