题目内容
18.解方程(1)x2-3x=0
(2)x2-10x=25.
分析 (1)利用提公因式法解一元二次方程;
(2)利用配方法解一元二次方程.
解答 解:(1)x2-3x=0
因式分解得x(x-3)=0,
x=0或x-3=0,
解得x1=0,x2=3;
(2)x2-10x=25
配方法因式分解得x2-10x+25=50,即(x-5)2=50,
开方得x-5=±5$\sqrt{2}$,
解得x1=5+5$\sqrt{2}$,x2=5-5$\sqrt{2}$;
点评 本题主要考查了利用因式分解解一元二次方程,解题的关键是熟记提公因式法及配方法.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
8.据调查,2011年5月茶陵县的房价均价为2600元/m2,2013年同期将达到3200元/m2,假设这两年茶陵县房价的平均增长率为x,根据题意,所列方程为( )
| A. | 2600(1+x%)2=3200 | B. | 2600(1-x%)2=3200 | C. | 2600(1+x)2=3200 | D. | 2600(1+x)2=3200 |
9.方程$\frac{x+1}{2}-\frac{x}{4}=1$的解为( )
| A. | x=-1 | B. | x=0 | C. | x=1 | D. | x=2 |
10.甲,乙两人练习跑步,若乙先跑10米,则甲跑5秒就可以追上乙;如果乙先跑2秒,甲跑4秒就可以追上乙.设甲的速度为x米/秒,乙的速度为y米/秒,根据题意,下列选项中所列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{5x-5y=10}\\{4x=2y+4y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{5x-5y=10}\\{4x-2=4y}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{5x-5y=10}\\{4x-2x=4y}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{5x+10=5y}\\{4x-2=4y}\end{array}\right.$ |
8.下列不等式中是一元一次不等式的是( )
| A. | $\frac{1}{3}$x-y<1 | B. | x2+5x-1≥0 | C. | $\frac{1}{x}$>3 | D. | $\frac{1}{2}$x<$\frac{1}{3}$-x |
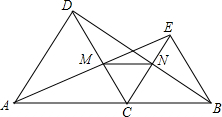 如图,已知C是线段AB上的任意一点(端点除外),分别以AC、BC为边并且在AB的同一侧作等边△ACD和等边△BCE,连接AE交CD于M,连接BD交CE于N.给出以下四个结论:①AE=BD;②CN=CM;③MN∥AB;④ME=NB.其中正确结论的个数是4.
如图,已知C是线段AB上的任意一点(端点除外),分别以AC、BC为边并且在AB的同一侧作等边△ACD和等边△BCE,连接AE交CD于M,连接BD交CE于N.给出以下四个结论:①AE=BD;②CN=CM;③MN∥AB;④ME=NB.其中正确结论的个数是4.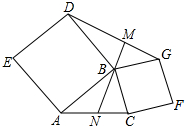 若以△ABC的边AB,BC为边向三角形外作正方形ABDE,BCFG,N为AC中点,求证:DG=2BN,BM⊥DG.
若以△ABC的边AB,BC为边向三角形外作正方形ABDE,BCFG,N为AC中点,求证:DG=2BN,BM⊥DG. 甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中:
甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中: