题目内容
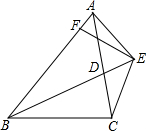 已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF.其中正确的是( )
已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF.其中正确的是( )| A、①②③ | B、①③④ |
| C、①②④ | D、①②③④ |
考点:全等三角形的判定与性质
专题:常规题型
分析:易证△ABD≌△EBC,可得∠BCE=∠BDA,AD=EC可得①②正确,再根据角平分线的性质可求得∠DAE=∠DCE,即③正确,根据③可求得④正确.
解答:解:
①∵BD为△ABC的角平分线,∴∠ABD=∠CBD,
∴在△ABD和△EBC中,
,
∴△ABD≌△EBC(SAS),…①正确;
②∵BD为△ABC的角平分线,BD=BC,BE=BA,
∴∠BCD=∠BDC=∠BAE=∠BEA,
∵△ABD≌△EBC,∴∠BCE=∠BDA,
∴∠BCE+∠BCD=∠BDA+∠BDC=180° …②正确;
③∵∠BCE=∠BDA,∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,∠BCD=∠BEA,
∴∠DCE=∠DAE,
∴△ACE为等腰三角形
∴AE=EC,
∵△ABD≌△EBC
∴AD=EC,
∴AD=AE=EC.…③正确;
④过E作EG⊥BC于G点,
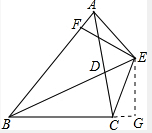
∵E是BD上的点,∴EF=EG,
∵在RT△BEG和RT△BEF中,
,
∴RT△BEG≌RT△BEF(HL),
∴BG=BF,
∵在RT△CEG和RT△AFE中,
,
∴RT△CEG≌RT△AFE(HL),
∴AF=CG,
∴BA+BC=BF+FA+BG-CG=BF+BG=2BF.…④正确.
故选D.
①∵BD为△ABC的角平分线,∴∠ABD=∠CBD,
∴在△ABD和△EBC中,
|
∴△ABD≌△EBC(SAS),…①正确;
②∵BD为△ABC的角平分线,BD=BC,BE=BA,
∴∠BCD=∠BDC=∠BAE=∠BEA,
∵△ABD≌△EBC,∴∠BCE=∠BDA,
∴∠BCE+∠BCD=∠BDA+∠BDC=180° …②正确;
③∵∠BCE=∠BDA,∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,∠BCD=∠BEA,
∴∠DCE=∠DAE,
∴△ACE为等腰三角形
∴AE=EC,
∵△ABD≌△EBC
∴AD=EC,
∴AD=AE=EC.…③正确;
④过E作EG⊥BC于G点,

∵E是BD上的点,∴EF=EG,
∵在RT△BEG和RT△BEF中,
|
∴RT△BEG≌RT△BEF(HL),
∴BG=BF,
∵在RT△CEG和RT△AFE中,
|
∴RT△CEG≌RT△AFE(HL),
∴AF=CG,
∴BA+BC=BF+FA+BG-CG=BF+BG=2BF.…④正确.
故选D.
点评:本题考查了全等三角形的判定,考查了全等三角形的对应边、对应角相等的性质,本题中熟练求证三角形全等和熟练运用全等三角形对应角、对应边相等性质是解题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 如图所示,其中的图(2)可以看作是由图(1)经过
如图所示,其中的图(2)可以看作是由图(1)经过 已知:如图,正方形ABCD的边长为6
已知:如图,正方形ABCD的边长为6 如图,直线BC与MN相交于点O,AO⊥BC,OE平分∠BON,若∠EON=21°,求∠AOM的度数.
如图,直线BC与MN相交于点O,AO⊥BC,OE平分∠BON,若∠EON=21°,求∠AOM的度数.
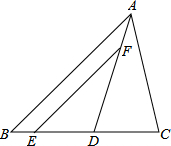 如图,在△ABC,AD平分∠BAC,E、F分别在BD、AD上,且DE=CD,EF=AC,求证:EF∥AB.
如图,在△ABC,AD平分∠BAC,E、F分别在BD、AD上,且DE=CD,EF=AC,求证:EF∥AB.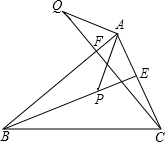 如图所示,CF、BE是△ABC的高,且BP=AC,CQ=AB,
如图所示,CF、BE是△ABC的高,且BP=AC,CQ=AB,