题目内容
如图①,A,B,C三点在一直线上,分别以AB、BC为边在AC同侧作等边△ABD和等边△BCE,AE交BD于点F,DC交BE于点G.
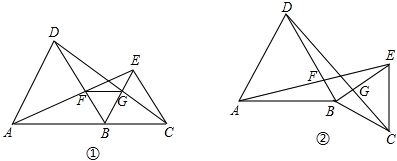
(1)判断AE=DC,BF=BG是否成立,并说明理由;
(2)如图②,若A,B,C不在同一直线上,那么这时上述结论成立吗?若成立请证明;
(3)判断△BFG的形状,并说明理由.

(1)判断AE=DC,BF=BG是否成立,并说明理由;
(2)如图②,若A,B,C不在同一直线上,那么这时上述结论成立吗?若成立请证明;
(3)判断△BFG的形状,并说明理由.
考点:全等三角形的判定与性质,等边三角形的判定与性质
专题:常规题型
分析:(1)易证△ABE≌△DBC,可得∠BDC=∠BAE,AE=DC,可证△BAF≌△BDG,可得BF=BG;
(2)AE=DC,但BF≠BG.
(3)根据等边三角形判定方法判定.
(2)AE=DC,但BF≠BG.
(3)根据等边三角形判定方法判定.
解答:解:(1)∵△ABD、△BCE都是等边三角形
∴AB=BD,BE=BC,∠ABD=∠CBE=60°,
∴∠ABE=∠CBD,
在△ABE和△DBC中,
,
∴△ABE≌△DBC(SAS),
∴AE=DC.∠BDC=∠BAE
在△BAF和△BDG中,
,
∴△BAF≌△BDG(ASA),
∴BF=BG.
(2)AE=DC,但BF≠BG.
理由①AE=DC.
∵△ABD和等边△BCE,
∴AB=BD,BC=BE,∠ABD=∠CBE=60°,
∴∠ABD+∠DBE=∠CBE+∠DBE,
即∠ABE=∠CBD,
在△ABE和△DBC中,
,
∴△ABE≌△DBC(SAS).
∴AE=DC(全等三角形对应边相等),
∠BAE=∠BDC(全等三角形对应角相等).
②BF≠BG.
理由:若BG=BF,由(1)可知△ABE≌△DBC,
∴∠BAF=∠BDG,
又AB=DB
则△ABF与△DBG有两边和一边的对角对应相等.
∴∠ABF=∠DBG或∠ABG+∠DBG=180°(不合题意,舍去)
∴△ABF≌△DBG(SAS).
∴∠ABF=∠DBG=60°(全等三角形对应角相等).
∴∠ABF=∠DBG=60°=∠CBE,
所以A、B、C在同一条直线上,这与题意A、B、C不在同一直线上矛盾,
∴BF≠BG.
(3)∵BF=BG,∠FBG=60°
∴∠BFG=∠BGF=∠FBG=60°
∴△BFG为等边三角形.
∴AB=BD,BE=BC,∠ABD=∠CBE=60°,
∴∠ABE=∠CBD,
在△ABE和△DBC中,
|
∴△ABE≌△DBC(SAS),
∴AE=DC.∠BDC=∠BAE
在△BAF和△BDG中,
|
∴△BAF≌△BDG(ASA),
∴BF=BG.
(2)AE=DC,但BF≠BG.
理由①AE=DC.
∵△ABD和等边△BCE,
∴AB=BD,BC=BE,∠ABD=∠CBE=60°,
∴∠ABD+∠DBE=∠CBE+∠DBE,
即∠ABE=∠CBD,
在△ABE和△DBC中,
|
∴△ABE≌△DBC(SAS).
∴AE=DC(全等三角形对应边相等),
∠BAE=∠BDC(全等三角形对应角相等).
②BF≠BG.
理由:若BG=BF,由(1)可知△ABE≌△DBC,
∴∠BAF=∠BDG,
又AB=DB
则△ABF与△DBG有两边和一边的对角对应相等.
∴∠ABF=∠DBG或∠ABG+∠DBG=180°(不合题意,舍去)
∴△ABF≌△DBG(SAS).
∴∠ABF=∠DBG=60°(全等三角形对应角相等).
∴∠ABF=∠DBG=60°=∠CBE,
所以A、B、C在同一条直线上,这与题意A、B、C不在同一直线上矛盾,
∴BF≠BG.
(3)∵BF=BG,∠FBG=60°
∴∠BFG=∠BGF=∠FBG=60°
∴△BFG为等边三角形.
点评:本题考查了全等三角形的判定与性质及等边三角形的性质;证明线段不相等是比较独特的,要注意掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2008年9月27日,神舟七号航天员翟志刚完成中国历史上第一次太空行走,他相对地球行走了5 100千米路程,用科学记数法表示为( )
| A、51×102米 |
| B、5.1×103米 |
| C、5.1×106米 |
| D、0.51×107米 |
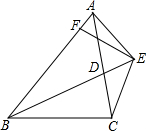 已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF.其中正确的是( )
已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF.其中正确的是( )| A、①②③ | B、①③④ |
| C、①②④ | D、①②③④ |
 如图,AB=CD,AD=CB,那么下列结论中错误的是( )
如图,AB=CD,AD=CB,那么下列结论中错误的是( )| A、∠A=∠C |
| B、AB=AD |
| C、AD∥BC |
| D、AB∥CD |
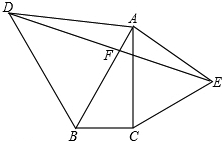 如图,在△ABC中,∠ABC=60°,分别以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接DE,交AB于点F,求证:DF=EF.
如图,在△ABC中,∠ABC=60°,分别以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接DE,交AB于点F,求证:DF=EF.