题目内容
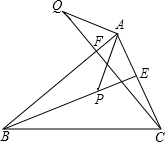 如图所示,CF、BE是△ABC的高,且BP=AC,CQ=AB,
如图所示,CF、BE是△ABC的高,且BP=AC,CQ=AB,(1)试说明AP与AQ的关系;
(2)题中的△ABC改为钝角三角形,其它条件不变,上述结论还正确吗?请画图并证明你的结论.
考点:全等三角形的判定与性质
专题:常规题型
分析:(1)根据题干给出条件可以求得∠ABE=∠ACQ,可证△ACQ≌△PBA,可得AP=AQ;
(2)按照题意作出图形,可以求得∠ABE=∠ACQ,可证△ACQ≌△PBA,可得AP=AQ;
(2)按照题意作出图形,可以求得∠ABE=∠ACQ,可证△ACQ≌△PBA,可得AP=AQ;
解答:解:(1)∵CF、BE是△ABC的高,
∴∠ABE+∠BAE=90°,∠ACQ+∠BAE=90°,
∴∠ABE=∠ACQ,
∵在△ACQ和△PBA中
,
∴△ACQ≌△PBA,(SAS)
∴AP=AQ,∠Q=∠BAP,
∵∠Q+∠QAB=90°,
∴∠BAP+∠QAB=90°,
∴AP⊥AQ;
(2)
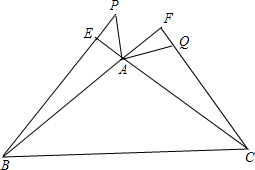
∵CF、BE是△ABC的高,∠ABE+∠AEB=∠BAC,∠ACQ+∠AFC=90°,
∴∠ABE=∠ACQ,
∵在△ACQ和△PBA中
,
∴△ACQ≌△PBA,(SAS)
∴AP=AQ,∠P=∠CAQ,
∵∠P+∠PAE=90°,
∴∠CAQ+∠PAE=90°,
∴∠PAQ=90°,
∴PA⊥AQ.
∴∠ABE+∠BAE=90°,∠ACQ+∠BAE=90°,
∴∠ABE=∠ACQ,
∵在△ACQ和△PBA中
|
∴△ACQ≌△PBA,(SAS)
∴AP=AQ,∠Q=∠BAP,
∵∠Q+∠QAB=90°,
∴∠BAP+∠QAB=90°,
∴AP⊥AQ;
(2)

∵CF、BE是△ABC的高,∠ABE+∠AEB=∠BAC,∠ACQ+∠AFC=90°,
∴∠ABE=∠ACQ,
∵在△ACQ和△PBA中
|
∴△ACQ≌△PBA,(SAS)
∴AP=AQ,∠P=∠CAQ,
∵∠P+∠PAE=90°,
∴∠CAQ+∠PAE=90°,
∴∠PAQ=90°,
∴PA⊥AQ.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ACQ≌△PBA是解题的关键.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
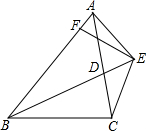 已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF.其中正确的是( )
已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF.其中正确的是( )| A、①②③ | B、①③④ |
| C、①②④ | D、①②③④ |
 如图,AB=CD,AD=CB,那么下列结论中错误的是( )
如图,AB=CD,AD=CB,那么下列结论中错误的是( )| A、∠A=∠C |
| B、AB=AD |
| C、AD∥BC |
| D、AB∥CD |
在同一平面直角坐标系中,函数y=
与函数y=-x的图象交点个数是( )
| 1 |
| x |
| A、0个 | B、1个 | C、2个 | D、3个 |
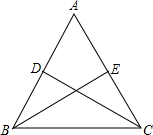 已知:△ABC中,AB=AC,D、E分别为AB、AC的中点,求证:∠ABE=∠ACD.
已知:△ABC中,AB=AC,D、E分别为AB、AC的中点,求证:∠ABE=∠ACD.