题目内容
14.有理数a,b,c在数轴上的位置如图所示,请化简:|a+b|+|b+c|-|a-c|.
分析 由数轴上点的位置及有理数的加减法则判断出绝对值里边式子的正负,利用绝对值的代数意义化简,去括号合并即可得到结果.
解答 解:由数轴上点的位置得:b<c<0<a,|a|<|c|<|b|,
所以a+b<0,b+c<0,a-c>0,
则|a+b|+|b+c|-|a-c|
=-(a+b)-(b+c)-(a-c)
=-a-b-b-c-a+c
=-2a-2b.
点评 此题考查了整式的加减,数轴,以及绝对值,涉及的知识有:去括号法则,以及合并同类项法则,熟练掌握法则是解本题的关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
4.若1是方程x2-2x+m=0的解,则m的值( )
| A. | 0 | B. | 1 | C. | -1 | D. | $\frac{1}{2}$ |
19.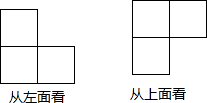 一个几何体由几个大小相同的小立方块搭成,从左面和从上面看到的这个几何体的形状如图所示,那么构成这个几何体的小立方块最多有( )个.
一个几何体由几个大小相同的小立方块搭成,从左面和从上面看到的这个几何体的形状如图所示,那么构成这个几何体的小立方块最多有( )个.
 一个几何体由几个大小相同的小立方块搭成,从左面和从上面看到的这个几何体的形状如图所示,那么构成这个几何体的小立方块最多有( )个.
一个几何体由几个大小相同的小立方块搭成,从左面和从上面看到的这个几何体的形状如图所示,那么构成这个几何体的小立方块最多有( )个.| A. | 4个 | B. | 5个 | C. | 6个 | D. | 无法确定 |
 如图所示,已知AC、BD相交于点O,OC=OA,OB=OD,则图中全等的三角形有4对.
如图所示,已知AC、BD相交于点O,OC=OA,OB=OD,则图中全等的三角形有4对. 如图,数学课上老师让同学们想办法测量学校国旗旗杆的高度,小明在阳光下走进旗杆的影子里,使自己的影子刚好被旗杆的影子遮住,已知小明的身高CD=1.70m,影长PD=2.2m,小明距旗杆底部的距离是19.8m,你能求出旗杆的高度AB吗?
如图,数学课上老师让同学们想办法测量学校国旗旗杆的高度,小明在阳光下走进旗杆的影子里,使自己的影子刚好被旗杆的影子遮住,已知小明的身高CD=1.70m,影长PD=2.2m,小明距旗杆底部的距离是19.8m,你能求出旗杆的高度AB吗?