题目内容
16.先化简,再求值:$\frac{{x}^{2}-1}{x}$÷(1-$\frac{2x-1}{x}$),其中x=$\sqrt{2}$-1.分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=$\frac{(x+1)(x-1)}{x}$÷$\frac{x-2x+1}{x}$
=$\frac{(x+1)(x-1)}{x}$•$\frac{x}{1-x}$
=-x-1,
当x=$\sqrt{2}$-1时,原式=-$\sqrt{2}$+1-1=-$\sqrt{2}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.下列用数轴表示不等式2-x≤1的解集正确的是( )
| A. | 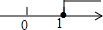 | B. |  | C. |  | D. |  |
 如图,点G是△ABC的重心,下列结论:①$\frac{DG}{GB}=\frac{1}{2}$;②$\frac{AE}{EB}=\frac{ED}{BC}$;③△EDG∽△CGB;④$\frac{{S}_{四边形AEGD}}{{S}_{△ABC}}=\frac{1}{3}$.其中正确的个数有( )
如图,点G是△ABC的重心,下列结论:①$\frac{DG}{GB}=\frac{1}{2}$;②$\frac{AE}{EB}=\frac{ED}{BC}$;③△EDG∽△CGB;④$\frac{{S}_{四边形AEGD}}{{S}_{△ABC}}=\frac{1}{3}$.其中正确的个数有( )
 如图的广义三阶幻方中,给出了3个数,则x的值为8.
如图的广义三阶幻方中,给出了3个数,则x的值为8.