Question

9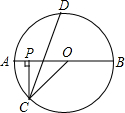．如图，P是⊙O的直径AB上的一点，PC⊥AB，PC交⊙O于C，∠OCP的平分线交⊙O于D，求证：$\widehat{AD}$=$\widehat{BD}$．

Answer 1

分析 首先连接OD，由OC=OD与∠OCP的平分线交⊙O于D，易证得∠PCD=∠PCO=∠D，则可得OD∥PC，继而证得OD⊥AB，然后由垂径定理证得结论．

解答 证明：连接OD，
∵OC=OD，
∴∠D=∠OCD，
∵CD平分∠OCP，
∴∠OCD=∠PCD，
∴∠PCD=∠D，
∴CP∥OD，
∵PC⊥AB，
∴OD⊥AB，
∵$\widehat{AD}$=$\widehat{BD}$．

点评 此题考查了垂径定理以及平行线的判定与性质．注意准确作出辅助线是解此题的关键．